8.6 Parametric equations  (Page 3/6)

Eliminating the parameter

In many cases, we may have a pair of parametric equations but find that it is simpler to draw a curve if the equation involves only two variables, such as $x$ and $y.$ Eliminating the parameter is a method that may make graphing some curves easier. However, if we are concerned with the mapping of the equation according to time, then it will be necessary to indicate the orientation of the curve as well. There are various methods for eliminating the parameter $t$ from a set of parametric equations; not every method works for every type of equation. Here we will review the methods for the most common types of equations.

Eliminating the parameter from polynomial, exponential, and logarithmic equations

For polynomial, exponential, or logarithmic equations expressed as two parametric equations, we choose the equation that is most easily manipulated and solve for $t.$ We substitute the resulting expression for $t$ into the second equation. This gives one equation in $x$ and $y.$

Eliminating the parameter from trigonometric equations

Eliminating the parameter from trigonometric equations is a straightforward substitution. We can use a few of the familiar trigonometric identities and the Pythagorean Theorem.

First, we use the identities:

Solving for $\cos t$ and $\sin t,$ we have

Then, use the Pythagorean Theorem:

Substituting gives

Eliminating the parameter from a pair of trigonometric parametric equations

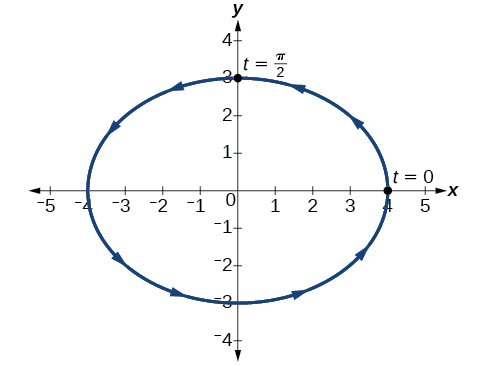
Eliminate the parameter from the given pair of trigonometric equations where $0\le t\le 2\pi$ and sketch the graph.

$\begin{array}{l}x(t)=4\cos t\\ y(t)=3\sin t\end{array}$

Solving for $\cos t$ and $\sin t,$ we have

$\begin{array}{l}x=4\cos t\hfill \\ \frac{x}{4}=\cos t\hfill \\ y=3\sin t\hfill \\ \frac{y}{3}=\sin t\hfill \end{array}$

Next, use the Pythagorean identity and make the substitutions.

$$\begin{array}{r}\hfill {\cos }^{2}t+{\sin }^{2}t=1\\ \hfill {\left(\frac{x}{4}\right)}^2+{\left(\frac{y}{3}\right)}^2=1\\ \hfill \frac{x^2}{16}+\frac{y^2}{9}=1\end{array}$$

The graph for the equation is shown in [link] .

Got questions? Get instant answers now!

Got questions? Get instant answers now!