1. Home
  2. Precalculus
  3. Introduction to calculus
  4. Derivatives

12.4 Derivatives  (Page 2/18)

<< Chapter < Page
  Precalculus     Page 2 / 18
Chapter >> Page >

Finding the average rate of change

Find the average rate of change connecting the points   ( 2 , −6 )   and   ( −1 , 5 ) .

We know the average rate of change connecting two points may be given by

AROC = f ( a + h ) − f ( a ) h .

If one point is   ( 2 , − 6 ) , or   ( 2 , f ( 2 ) ) , then   f ( 2 ) = −6.

The value   h   is the displacement from   2   to   − 1 , which equals   − 1 − 2 = −3.

For the other point,   f ( a + h )   is the y -coordinate at   a + h , which is   2 + ( −3 )   or   −1 , so   f ( a + h ) = f ( −1 ) = 5.

AROC = f ( a + h ) − f ( a ) h             = 5 − ( − 6 ) − 3             = 11 − 3             = − 11 3
Got questions? Get instant answers now!
Got questions? Get instant answers now!

Find the average rate of change connecting the points   ( − 5 , 1.5 )   and   ( − 2.5 , 9 ) .

3

Got questions? Get instant answers now!

Understanding the instantaneous rate of change

Now that we can find the average rate of change, suppose we make   h   in [link] smaller and smaller. Then   a + h   will approach   a   as   h   gets smaller, getting closer and closer to 0. Likewise, the second point   ( a + h , f ( a + h ) )   will approach the first point,   ( a , f ( a ) ) .   As a consequence, the connecting line between the two points, called the secant line, will get closer and closer to being a tangent to the function at   x = a , and the slope of the secant line will get closer and closer to the slope of the tangent at   x = a .   See [link] .

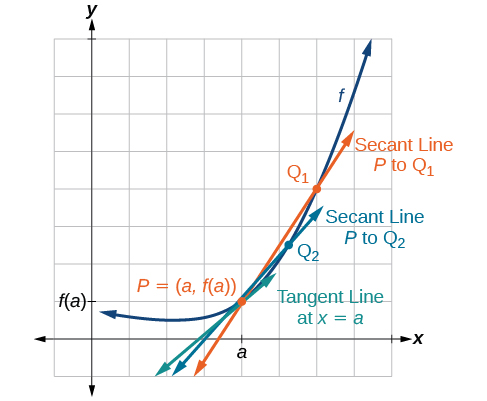
Graph of an increasing function that contains a point, P, at (a, f(a)). At the point, there is a tangent line and two secant lines where one secant line is connected to Q1 and another secant line is connected to Q2.
The connecting line between two points moves closer to being a tangent line at   x = a .

Because we are looking for the slope of the tangent at   x = a , we can think of the measure of the slope of the curve of a function   f   at a given point as the rate of change at a particular instant. We call this slope the instantaneous rate of change , or the derivative of the function at   x = a .   Both can be found by finding the limit of the slope of a line connecting the point at   x = a   with a second point infinitesimally close along the curve. For a function   f   both the instantaneous rate of change of the function and the derivative of the function at   x = a   are written as   f ' ( a ) , and we can define them as a two-sided limit    that has the same value whether approached from the left or the right.

f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h

The expression by which the limit is found is known as the difference quotient .

Definition of instantaneous rate of change and derivative

The derivative    , or instantaneous rate of change    , of a function   f   at   x = a , is given by

f ' ( a ) = lim h → 0 f ( a + h ) − f ( a ) h

The expression   f ( a + h ) − f ( a ) h   is called the difference quotient.

We use the difference quotient to evaluate the limit of the rate of change of the function as   h   approaches 0.

Derivatives: interpretations and notation

The derivative    of a function can be interpreted in different ways. It can be observed as the behavior of a graph of the function or calculated as a numerical rate of change of the function.

  • The derivative of a function   f ( x )   at a point   x = a   is the slope of the tangent line to the curve   f ( x )   at   x = a .   The derivative of   f ( x )   at   x = a   is written   f ′ ( a ) .
  • The derivative   f ′ ( a )   measures how the curve changes at the point   ( a , f ( a ) ) .
  • The derivative   f ′ ( a )   may be thought of as the instantaneous rate of change of the function   f ( x )   at   x = a .
  • If a function measures distance as a function of time, then the derivative measures the instantaneous velocity at time   t = a .

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Precalculus. OpenStax CNX. Jan 19, 2016 Download for free at https://legacy.cnx.org/content/col11667/1.6
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Precalculus' conversation and receive update notifications?

Ask