| << Chapter < Page | Chapter >> Page > |
For the following exercises, find the limits if and
For the following exercises, evaluate the limits using algebraic techniques.
For the following exercises, use numerical evidence to determine whether the limit exists at If not, describe the behavior of the graph of the function at
For the following exercises, determine where the given function is continuous. Where it is not continuous, state which conditions fail, and classify any discontinuities.
removable discontinuity at is not defined, but limits exist.
For the following exercises, find the average rate of change
For the following exercises, find the derivative of the function.
Find the equation of the tangent line to the graph of
at the indicated
value.
;
For the following exercises, with the aid of a graphing utility, explain why the function is not differentiable everywhere on its domain. Specify the points where the function is not differentiable.
Given that the volume of a right circular cone is and that a given cone has a fixed height of 9 cm and variable radius length, find the instantaneous rate of change of volume with respect to radius length when the radius is 2 cm. Give an exact answer in terms of
For the following exercises, use the graph of in [link] .
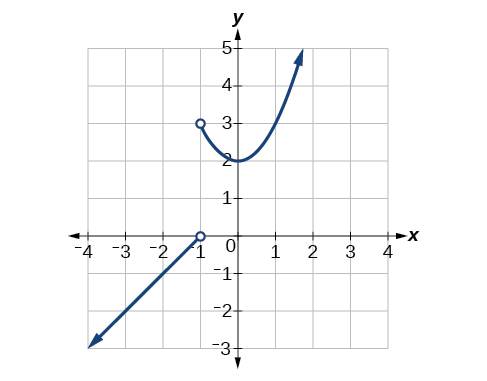
At what values of is discontinuous? What property of continuity is violated?
For the following exercises, with the use of a graphing utility, use numerical or graphical evidence to determine the left- and right-hand limits of the function given as approaches If the function has a limit as approaches state it. If not, discuss why there is no limit
and Thus, the limit of the function as approaches 2 does not exist.
For the following exercises, evaluate each limit using algebraic techniques.
For the following exercises, determine whether or not the given function is continuous. If it is continuous, show why. If it is not continuous, state which conditions fail.
For the following exercises, use the definition of a derivative to find the derivative of the given function at
For the graph in [link] , determine where the function is continuous/discontinuous and differentiable/not differentiable.
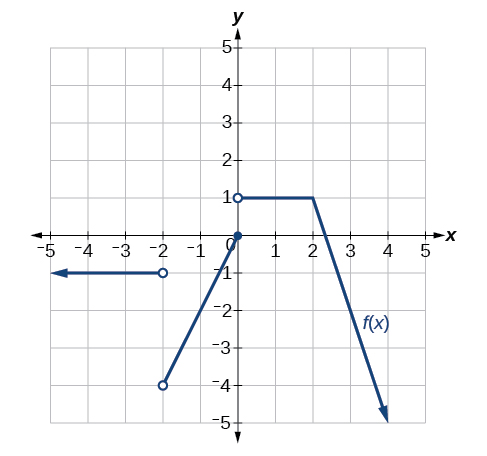
discontinuous at –2,0, not differentiable at –2,0, 2.
For the following exercises, with the aid of a graphing utility, explain why the function is not differentiable everywhere on its domain. Specify the points where the function is not differentiable.
For the following exercises, explain the notation in words when the height of a projectile in feet, is a function of time in seconds after launch and is given by the function
For the following exercises, use technology to evaluate the limit.
Evaluate the limit by hand.
At what value(s) of is the function below discontinuous?
For the following exercises, consider the function whose graph appears in [link] .
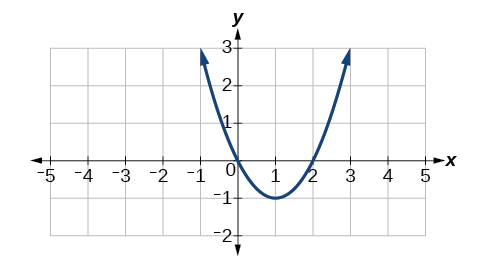
Find all values of at which does not exist.
Find an equation of the tangent line to the graph of the indicated point:
For the following exercises, use the function .
Graph the function by entering and then by entering .
Explore the behavior of the graph of around by graphing the function on the following domains, [0.9, 1.1], [0.99, 1.01], [0.999, 1.001], and [0.9999, 1.0001]. Use this information to determine whether the function appears to be differentiable at
The graph is not differentiable at (cusp).
For the following exercises, find the derivative of each of the functions using the definition:

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?