| << Chapter < Page | Chapter >> Page > |
Solve the given system of equations by addition.
Both equations are already set equal to a constant. Notice that the coefficient of in the second equation, –1, is the opposite of the coefficient of in the first equation, 1. We can add the two equations to eliminate without needing to multiply by a constant.
Now that we have eliminated we can solve the resulting equation for
Then, we substitute this value for into one of the original equations and solve for
The solution to this system is
Check the solution in the first equation.
Solve the given system of equations by the addition method .
Adding these equations as presented will not eliminate a variable. However, we see that the first equation has in it and the second equation has So if we multiply the second equation by the x -terms will add to zero.
Now, let’s add them.
For the last step, we substitute into one of the original equations and solve for
Our solution is the ordered pair See [link] . Check the solution in the original second equation.
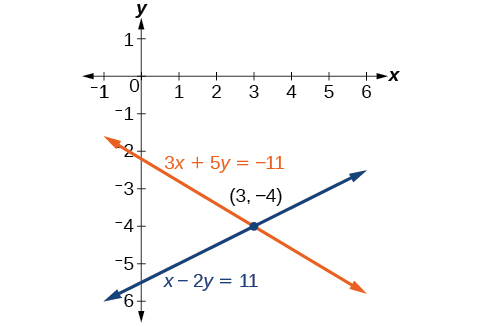
Solve the given system of equations in two variables by addition.
One equation has and the other has The least common multiple is so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate by multiplying the first equation by and the second equation by
Then, we add the two equations together.
Substitute into the original first equation.
The solution is Check it in the other equation.
See [link] .

Solve the given system of equations in two variables by addition.
First clear each equation of fractions by multiplying both sides of the equation by the least common denominator.
Now multiply the second equation by so that we can eliminate the x -variable.
Add the two equations to eliminate the x -variable and solve the resulting equation.
Substitute into the first equation.
The solution is Check it in the other equation.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?