5.3 The other trigonometric functions (Page 2/13)

Precalculus

Page 2 / 13

Try It

The point $(\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2})$ is on the unit circle, as shown in [link] . Find $\sin t, \cos t, \tan t, \sec t, \csc t,$ and $\cot t .$

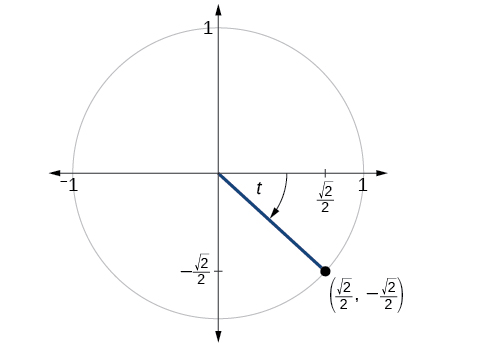
Graph of circle with angle of t inscribed. Point of (square root of 2 over 2, negative square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.

$\sin t = - \frac{\sqrt{2}}{2}, \cos t = \frac{\sqrt{2}}{2}, \tan t = - 1, \sec t = \sqrt{2}, \csc t = - \sqrt{2}, \cot t = - 1$

Got questions? Get instant answers now!

Finding the trigonometric functions of an angle

Find $\sin t, \cos t, \tan t, \sec t, \csc t,$ and $\cot t$ when $t = \frac{π}{6} .$

We have previously used the properties of equilateral triangles to demonstrate that $\sin \frac{π}{6} = \frac{1}{2}$ and $\cos \frac{π}{6} = \frac{\sqrt{3}}{2} .$ We can use these values and the definitions of tangent, secant, cosecant, and cotangent as functions of sine and cosine to find the remaining function values.

\begin{array}{l} \begin{array}{l} \tan \frac{π}{6} = \frac{\sin \frac{π}{6}}{\cos \frac{π}{6}} \end{array} \\ = \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3} \end{array}

\begin{array}{l} \sec \frac{π}{6} = \frac{1}{\cos \frac{π}{6}} \\ = \frac{1}{\frac{\sqrt{3}}{2}} = \frac{2}{\sqrt{3}} = \frac{2 \sqrt{3}}{3} \end{array}

\csc \frac{π}{6} = \frac{1}{\sin \frac{π}{6}} = \frac{1}{\frac{1}{2}} = 2

\begin{array}{l} \cot \frac{π}{6} = \frac{\cos \frac{π}{6}}{\sin \frac{π}{6}} \\ = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3} \end{array}

Got questions? Get instant answers now!

Try It

Find $\sin t, \cos t, \tan t, \sec t, \csc t,$ and $\cot t$ when $t = \frac{π}{3} .$

$\begin{array}{l} \sin \frac{π}{3} = \frac{\sqrt{3}}{2} \\ \cos \frac{π}{3} = \frac{1}{2} \\ \tan \frac{π}{3} = \sqrt{3} \\ \sec \frac{π}{3} = 2 \\ \csc \frac{π}{3} = \frac{2 \sqrt{3}}{3} \\ \cot \frac{π}{3} = \frac{\sqrt{3}}{3} \end{array}$

Got questions? Get instant answers now!

Because we know the sine and cosine values for the common first-quadrant angles, we can find the other function values for those angles as well by setting $x$ equal to the cosine and $y$ equal to the sine and then using the definitions of tangent, secant, cosecant, and cotangent. The results are shown in [link] .

Angle	$0$	$\frac{π}{6}, or 30°$	$\frac{π}{4}, or 45°$	$\frac{π}{3}, or 60°$	$\frac{π}{2}, or 90°$
Cosine	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
Sine	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
Tangent	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	Undefined
Secant	1	$\frac{2 \sqrt{3}}{3}$	$\sqrt{2}$	2	Undefined
Cosecant	Undefined	2	$\sqrt{2}$	$\frac{2 \sqrt{3}}{3}$	1
Cotangent	Undefined	$\sqrt{3}$	1	$\frac{\sqrt{3}}{3}$	0

Using reference angles to evaluate tangent, secant, cosecant, and cotangent

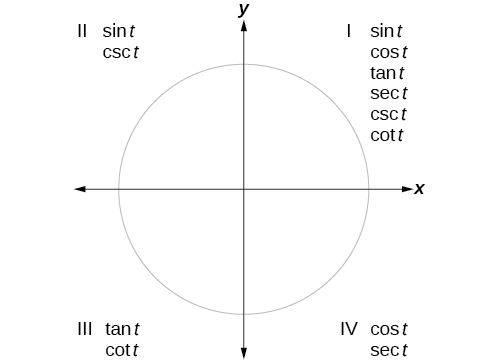
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles as we have already done with the sine and cosine functions. The procedure is the same: Find the reference angle formed by the terminal side of the given angle with the horizontal axis. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x - and y -values in the original quadrant. [link] shows which functions are positive in which quadrant.

To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “ A ,” a ll of the six trigonometric functions are positive. In quadrant II, “ S mart,” only s ine and its reciprocal function, cosecant, are positive. In quadrant III, “ T rig,” only t angent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “ C lass,” only c osine and its reciprocal function, secant, are positive.

Graph of circle with each quadrant labeled. Under quadrant 1, labels fro sin t, cos t, tan t, sec t, csc t, and cot t. Under quadrant 2, labels for sin t and csc t. Under quadrant 3, labels for tan t and cot t. Under quadrant 4, labels for cos t, sec t.

How To

Given an angle not in the first quadrant, use reference angles to find all six trigonometric functions.

Measure the angle formed by the terminal side of the given angle and the horizontal axis. This is the reference angle.
Evaluate the function at the reference angle.
Observe the quadrant where the terminal side of the original angle is located. Based on the quadrant, determine whether the output is positive or negative.

Using reference angles to find trigonometric functions

Use reference angles to find all six trigonometric functions of $- \frac{5 π}{6} .$

The angle between this angle’s terminal side and the x -axis is $\frac{π}{6},$ so that is the reference angle. Since $- \frac{5 π}{6}$ is in the third quadrant, where both $x$ and $y$ are negative, cosine, sine, secant, and cosecant will be negative, while tangent and cotangent will be positive.

\begin{array}{l} \cos (- \frac{5 π}{6}) = - \frac{\sqrt{3}}{2}, \sin (- \frac{5 π}{6}) = - \frac{1}{2}, tan (- \frac{5 π}{6}) = \frac{\sqrt{3}}{3} \\ sec (- \frac{5 π}{6}) = - \frac{2 \sqrt{3}}{3}, csc (- \frac{5 π}{6}) = - 2, \cot (- \frac{5 π}{6}) = \sqrt{3} \end{array}

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 6

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Precalculus. OpenStax CNX. Jan 19, 2016 Download for free at https://legacy.cnx.org/content/col11667/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Precalculus' conversation and receive update notifications?

Ask

	3 The other trigonometric functions By OpenStax Read Online Course
	1 The other trigonometric functions By OpenStax Read Online Course
	13 Sociology 13 Aging and the Elderly MCQ By OpenStax Start Quiz
	Basic Of Computer Exam By Naveen Tomar Start Quiz
	PE Power Enigeering Safety By Gerr Zen Start Quiz
	2 Psychology MCQ 2009 1 Exam By John Gabrieli Start Exam
	5 Neuroanatomy 05 Somesthetic Sensation By Stephen Voron Start Quiz
	Financial Markets By Keyaira Braxton Start Exam
	5 Psychology MCQ 2010 1 Exam By John Gabrieli Start Exam
	19 AP 19 Cardiovascular System Heart MCQ By OpenStax Start Quiz
	College algebra By OpenStax Read Online Course
	39 Biology 39 The Respiratory System MCQ By OpenStax Start Quiz