| << Chapter < Page | Chapter >> Page > |
Find the vertical asymptotes and removable discontinuities of the graph of
Removable discontinuity at Vertical asymptotes:
While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.
There are three distinct outcomes when checking for horizontal asymptotes:
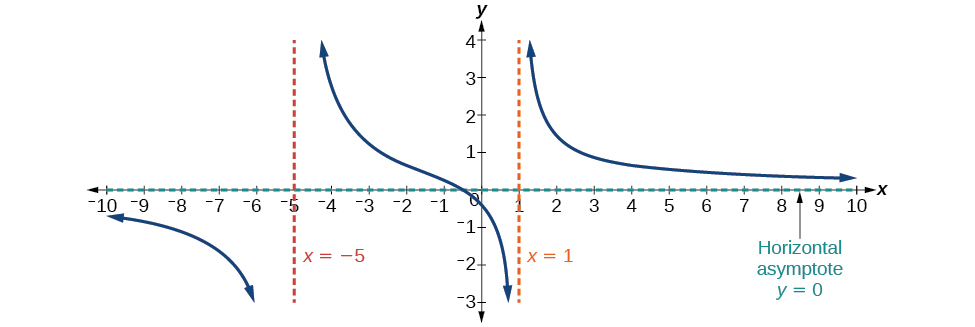
Case 1: If the degree of the denominator>degree of the numerator, there is a horizontal asymptote at
In this case, the end behavior is This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function and the outputs will approach zero, resulting in a horizontal asymptote at See [link] . Note that this graph crosses the horizontal asymptote.
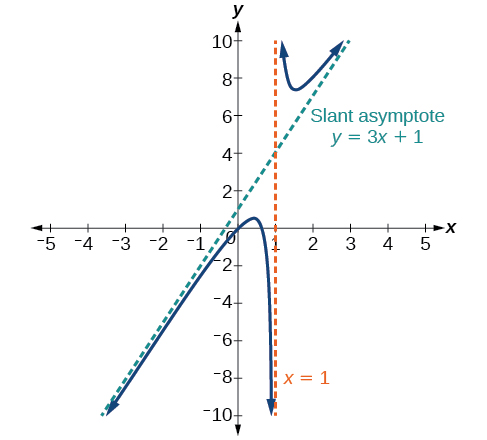
Case 2: If the degree of the denominator<degree of the numerator by one, we get a slant asymptote.
In this case, the end behavior is This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of looks like a diagonal line, and since will behave similarly to it will approach a line close to This line is a slant asymptote.
To find the equation of the slant asymptote, divide The quotient is and the remainder is 2. The slant asymptote is the graph of the line See [link] .
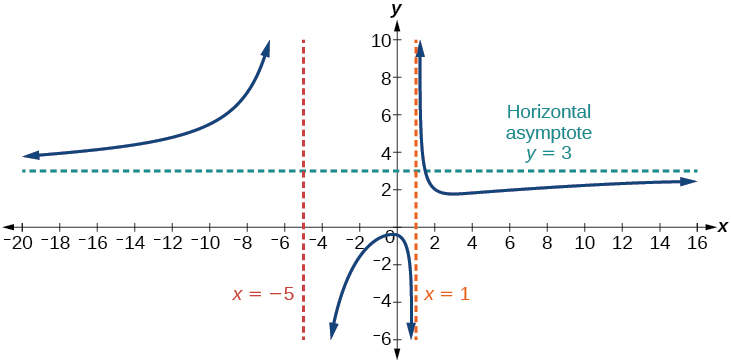
Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at where and are the leading coefficients of and for
In this case, the end behavior is This tells us that as the inputs grow large, this function will behave like the function which is a horizontal line. As resulting in a horizontal asymptote at See [link] . Note that this graph crosses the horizontal asymptote.
Notice that, while the graph of a rational function will never cross a vertical asymptote , the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?