| << Chapter < Page | Chapter >> Page > |
There is a similar relationship between the number of sign changes in and the number of negative real zeros.
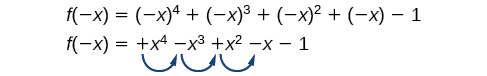
In this case, has 3 sign changes. This tells us that could have 3 or 1 negative real zeros.
According to Descartes’ Rule of Signs , if we let be a polynomial function with real coefficients:
Use Descartes’ Rule of Signs to determine the possible numbers of positive and negative real zeros for
Begin by determining the number of sign changes.
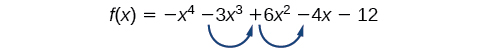
There are two sign changes, so there are either 2 or 0 positive real roots. Next, we examine to determine the number of negative real roots.
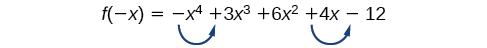
Again, there are two sign changes, so there are either 2 or 0 negative real roots.
There are four possibilities, as we can see in [link] .
| Positive Real Zeros | Negative Real Zeros | Complex Zeros | Total Zeros |
|---|---|---|---|
| 2 | 2 | 0 | 4 |
| 2 | 0 | 2 | 4 |
| 0 | 2 | 2 | 4 |
| 0 | 0 | 4 | 4 |
Use Descartes’ Rule of Signs to determine the maximum possible numbers of positive and negative real zeros for Use a graph to verify the numbers of positive and negative real zeros for the function.
There must be 4, 2, or 0 positive real roots and 0 negative real roots. The graph shows that there are 2 positive real zeros and 0 negative real zeros.
We have now introduced a variety of tools for solving polynomial equations. Let’s use these tools to solve the bakery problem from the beginning of the section.
A new bakery offers decorated sheet cakes for children’s birthday parties and other special occasions. The bakery wants the volume of a small cake to be 351 cubic inches. The cake is in the shape of a rectangular solid. They want the length of the cake to be four inches longer than the width of the cake and the height of the cake to be one-third of the width. What should the dimensions of the cake pan be?
Begin by writing an equation for the volume of the cake. The volume of a rectangular solid is given by We were given that the length must be four inches longer than the width, so we can express the length of the cake as We were given that the height of the cake is one-third of the width, so we can express the height of the cake as Let’s write the volume of the cake in terms of width of the cake.
Substitute the given volume into this equation.
Descartes' rule of signs tells us there is one positive solution. The Rational Zero Theorem tells us that the possible rational zeros are and We can use synthetic division to test these possible zeros. Only positive numbers make sense as dimensions for a cake, so we need not test any negative values. Let’s begin by testing values that make the most sense as dimensions for a small sheet cake. Use synthetic division to check
Since 1 is not a solution, we will check
![]()
Since 3 is not a solution either, we will test
![]()
Synthetic division gives a remainder of 0, so 9 is a solution to the equation. We can use the relationships between the width and the other dimensions to determine the length and height of the sheet cake pan.
The sheet cake pan should have dimensions 13 inches by 9 inches by 3 inches.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?