3.5 Dividing polynomials  (Page 2/6)

Using synthetic division to divide polynomials

As we’ve seen, long division of polynomials can involve many steps and be quite cumbersome. Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is 1.

To illustrate the process, recall the example at the beginning of the section.

Divide $2x^3-3x^2+4x+5$ by $x+2$ using the long division algorithm.

The final form of the process looked like this:

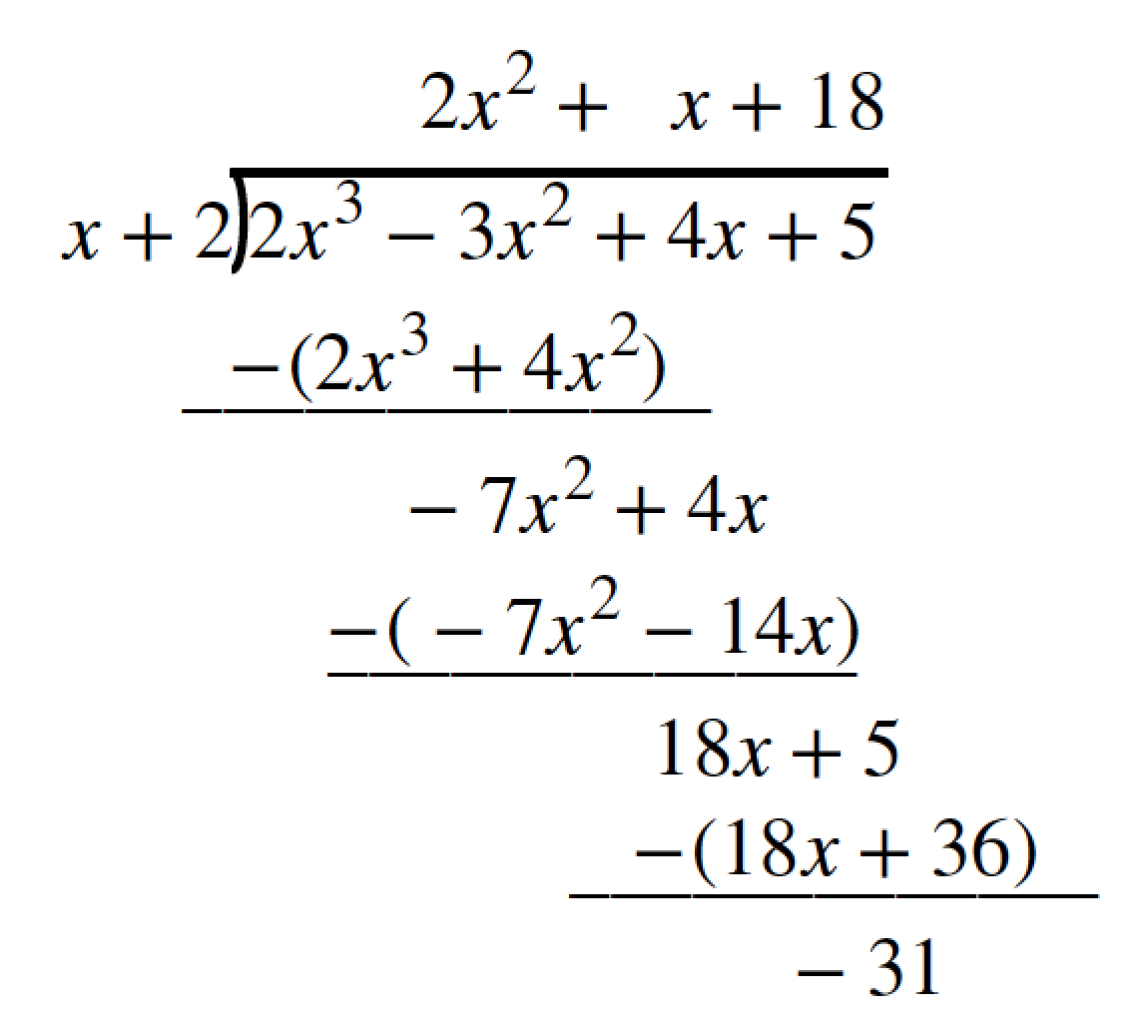
There is a lot of repetition in the table. If we don’t write the variables but, instead, line up their coefficients in columns under the division sign and also eliminate the partial products, we already have a simpler version of the entire problem.

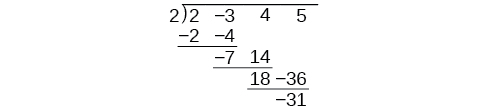
Synthetic division carries this simplification even a few more steps. Collapse the table by moving each of the rows up to fill any vacant spots. Also, instead of dividing by 2, as we would in division of whole numbers, then multiplying and subtracting the middle product, we change the sign of the “divisor” to –2, multiply and add. The process starts by bringing down the leading coefficient.

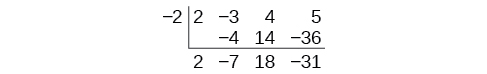
We then multiply it by the “divisor” and add, repeating this process column by column, until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the bottom row is the remainder. In this case, the quotient is $2x²–7x+18$ and the remainder is $\mathrm{–31.}$ The process will be made more clear in [link] .