8.5 Atomic spectra and x-rays  (Page 17/12)

The study of atomic spectra provides most of our knowledge about atoms. In modern science, atomic spectra are used to identify species of atoms in a range of objects, from distant galaxies to blood samples at a crime scene.

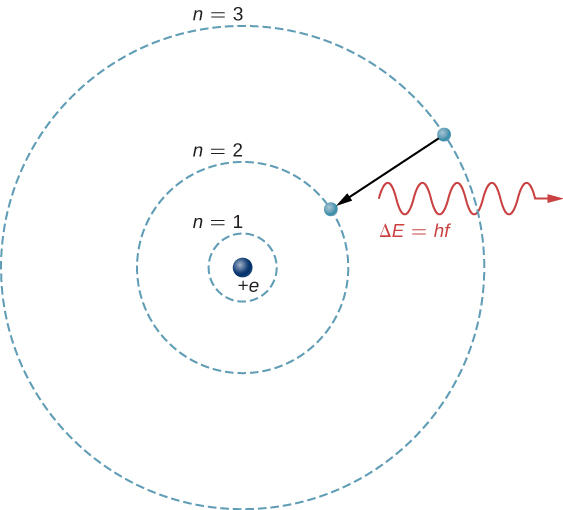
The theoretical basis of atomic spectroscopy is the transition of electrons between energy levels in atoms. For example, if an electron in a hydrogen atom makes a transition from the $n=3$ to the $n=2$ shell, the atom emits a photon with a wavelength

where $\text{Δ}E=E_3-E_2$ is energy carried away by the photon and $hc=1940\text{eV}·\text{nm}$ . After this radiation passes through a spectrometer, it appears as a sharp spectral line on a screen. The Bohr model of this process is shown in [link] . If the electron later absorbs a photon with energy $\text{Δ}E$ , the electron returns to the $n=3$ shell. (We examined the Bohr model earlier, in Photons and Matter Waves .)

To understand atomic transitions in multi-electron atoms, it is necessary to consider many effects, including the Coulomb repulsion between electrons and internal magnetic interactions (spin-orbit and spin-spin couplings). Fortunately, many properties of these systems can be understood by neglecting interactions between electrons and representing each electron by its own single-particle wave function ${\psi }_{nlm}$ .

Atomic transitions must obey selection rules    . These rules follow from principles of quantum mechanics and symmetry. Selection rules classify transitions as either allowed or forbidden. (Forbidden transitions do occur, but the probability of the typical forbidden transition is very small.) For a hydrogen-like atom, atomic transitions that involve electromagnetic interactions (the emission and absorption of photons) obey the following selection rule:

where l is associated with the magnitude of orbital angular momentum,

For multi-electron atoms, similar rules apply. To illustrate this rule, consider the observed atomic transitions in hydrogen (H), sodium (Na), and mercury (Hg) ( [link] ). The horizontal lines in this diagram correspond to atomic energy levels, and the transitions allowed by this selection rule are shown by lines drawn between these levels. The energies of these states are on the order of a few electron volts, and photons emitted in transitions are in the visible range. Technically, atomic transitions can violate the selection rule, but such transitions are uncommon.

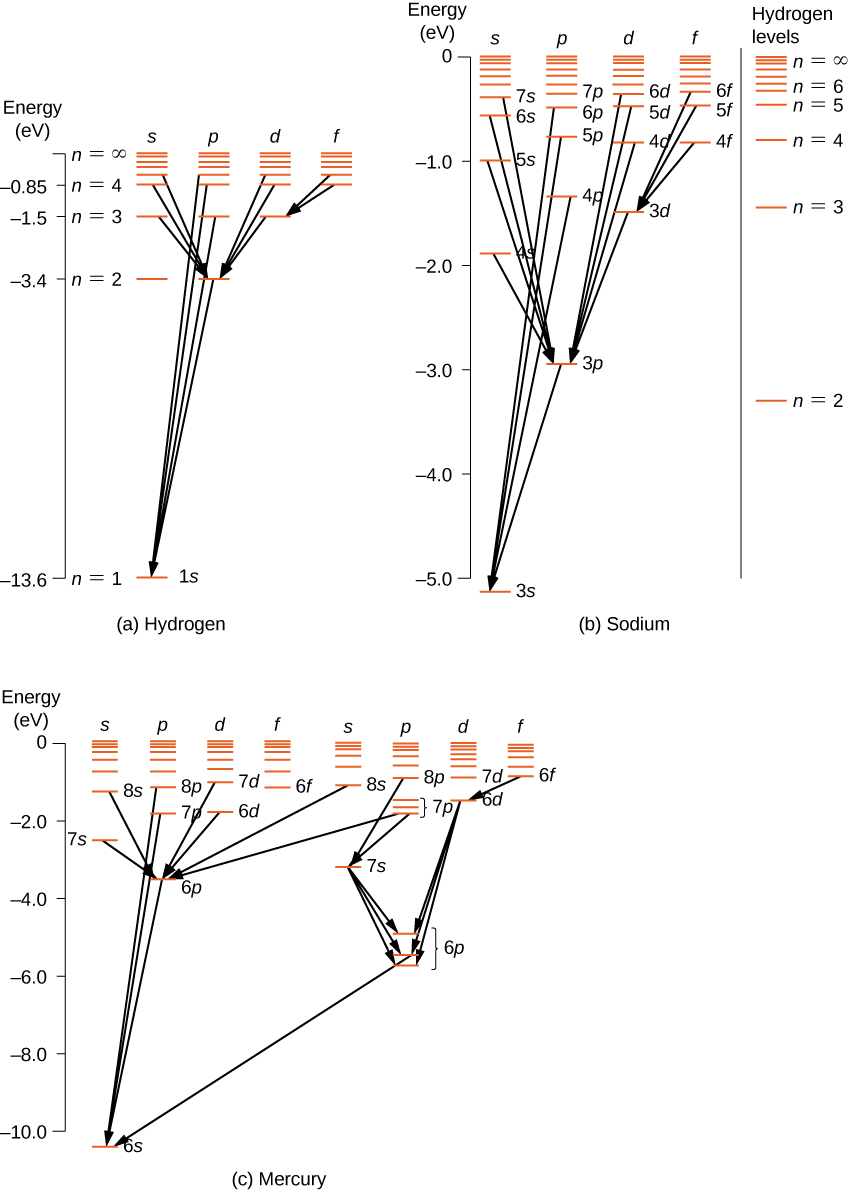
The hydrogen atom has the simplest energy-level diagram. If we neglect electron spin, all states with the same value of n have the same total energy. However, spin-orbit coupling splits the $n=2$ states into two angular momentum states ( s and p ) of slightly different energies. (These levels are not vertically displaced, because the energy splitting is too small to show up in this diagram.) Likewise, spin-orbit coupling splits the $n=3$ states into three angular momentum states ( s , p , and d ).