5.6 Relativistic velocity transformation  (Page 20/4)

Remaining in place in a kayak in a fast-moving river takes effort. The river current pulls the kayak along. Trying to paddle against the flow can move the kayak upstream relative to the water, but that only accounts for part of its velocity relative to the shore. The kayak’s motion is an example of how velocities in Newtonian mechanics combine by vector addition. The kayak’s velocity is the vector sum of its velocity relative to the water and the water’s velocity relative to the riverbank. However, the relativistic addition of velocities is quite different.

Velocity transformations

Imagine a car traveling at night along a straight road, as in [link] . The driver sees the light leaving the headlights at speed c within the car’s frame of reference. If the Galilean transformation applied to light, then the light from the car’s headlights would approach the pedestrian at a speed $u=v+c,$ contrary to Einstein’s postulates.

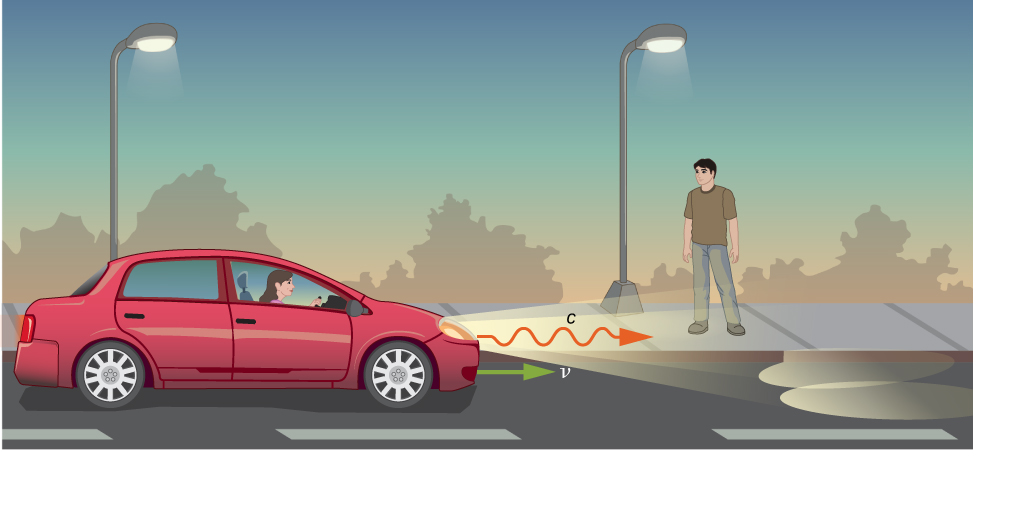
Both the distance traveled and the time of travel are different in the two frames of reference, and they must differ in a way that makes the speed of light the same in all inertial frames. The correct rules for transforming velocities from one frame to another can be obtained from the Lorentz transformation equations.

Relativistic transformation of velocity

Suppose an object P is moving at constant velocity $u=\left(u_x^{\prime },u_y^{\prime },u_z^{\prime }\right)$ as measured in the $S\prime$ frame. The $S\prime$ frame is moving along its $x\prime \text{-axis}$ at velocity v . In an increment of time $dt\prime$ , the particle is displaced by $dx\prime$ along the $x\prime \text{-axis.}$ Applying the Lorentz transformation equations gives the corresponding increments of time and displacement in the unprimed axes:

The velocity components of the particle seen in the unprimed coordinate system are then

We thus obtain the equations for the velocity components of the object as seen in frame S :

Compare this with how the Galilean transformation of classical mechanics says the velocities transform, by adding simply as vectors:

When the relative velocity of the frames is much smaller than the speed of light, that is, when $v\ll c,$ the special relativity velocity addition law reduces to the Galilean velocity law. When the speed v of $S\prime$ relative to S is comparable to the speed of light, the relativistic velocity addition    law gives a much smaller result than the classical (Galilean) velocity addition    does.