5.4 Length contraction  (Page 2/6)

The moving observer travels with the muon and therefore observes the proper time $\text{Δ}\tau .$ The two velocities are identical; thus,

We know that $\text{Δ}t=\gamma \text{Δ}\tau .$ Substituting this equation into the relationship above gives

Substituting for $\gamma$ gives an equation relating the distances measured by different observers.

If we measure the length of anything moving relative to our frame, we find its length L to be smaller than the proper length $L_0$ that would be measured if the object were stationary. For example, in the muon’s rest frame, the distance Earth moves between where the muon was produced and where it decayed is shorter than the distance traveled as seen from the Earth’s frame. Those points are fixed relative to Earth but are moving relative to the muon. Clouds and other objects are also contracted along the direction of motion as seen from muon’s rest frame.

Thus, two observers measure different distances along their direction of relative motion, depending on which one is measuring distances between objects at rest.

But what about distances measured in a direction perpendicular to the relative motion? Imagine two observers moving along their x -axes and passing each other while holding meter sticks vertically in the y -direction. [link] shows two meter sticks M and $\text{M}\prime$ that are at rest in the reference frames of two boys S and $\text{S}\prime ,$ respectively. A small paintbrush is attached to the top (the 100-cm mark) of stick $\text{M}\prime \text{.}$ Suppose that $\text{S}\prime$ is moving to the right at a very high speed v relative to S, and the sticks are oriented so that they are perpendicular, or transverse, to their relative velocity vector. The sticks are held so that as they pass each other, their lower ends (the 0-cm marks) coincide. Assume that when S looks at his stick M afterwards, he finds a line painted on it, just below the top of the stick. Because the brush is attached to the top of the other boy’s stick $\text{M}\prime \text{,}$ S can only conclude that stick $\text{M}\prime$ is less than 1.0 m long.

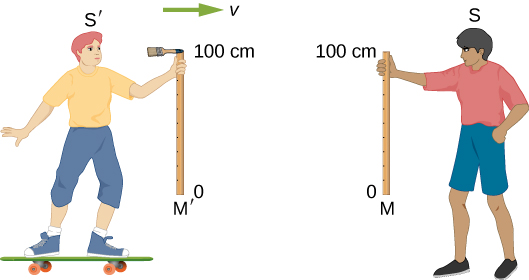
Now when the boys approach each other, $\text{S}\prime \text{,}$ like S, sees a meter stick moving toward him with speed v . Because their situations are symmetric, each boy must make the same measurement of the stick in the other frame. So, if S measures stick $\text{M}\prime$ to be less than 1.0 m long, $\text{S}\prime$ must measure stick M to be also less than 1.0 m long, and $\text{S}\prime$ must see his paintbrush pass over the top of stick M and not paint a line on it. In other words, after the same event, one boy sees a painted line on a stick, while the other does not see such a line on that same stick!

Einstein’s first postulate requires that the laws of physics (as, for example, applied to painting) predict that S and $\text{S}\prime \text{,}$ who are both in inertial frames, make the same observations; that is, S and $\text{S}\prime$ must either both see a line painted on stick M, or both not see that line. We are therefore forced to conclude our original assumption that S saw a line painted below the top of his stick was wrong! Instead, S finds the line painted right at the 100-cm mark on M. Then both boys will agree that a line is painted on M, and they will also agree that both sticks are exactly 1 m long. We conclude then that measurements of a transverse length must be the same in different inertial frames .