3.5 The michelson interferometer  (Page 23/7)

The Michelson interferometer    (invented by the American physicist Albert A. Michelson , 1852–1931) is a precision instrument that produces interference fringes by splitting a light beam into two parts and then recombining them after they have traveled different optical paths. [link] depicts the interferometer and the path of a light beam from a single point on the extended source S, which is a ground-glass plate that diffuses the light from a monochromatic lamp of wavelength ${\lambda }_0$ . The beam strikes the half-silvered mirror M, where half of it is reflected to the side and half passes through the mirror. The reflected light travels to the movable plane mirror ${\text{M}}_1$ , where it is reflected back through M to the observer. The transmitted half of the original beam is reflected back by the stationary mirror ${\text{M}}_2$ and then toward the observer by M.

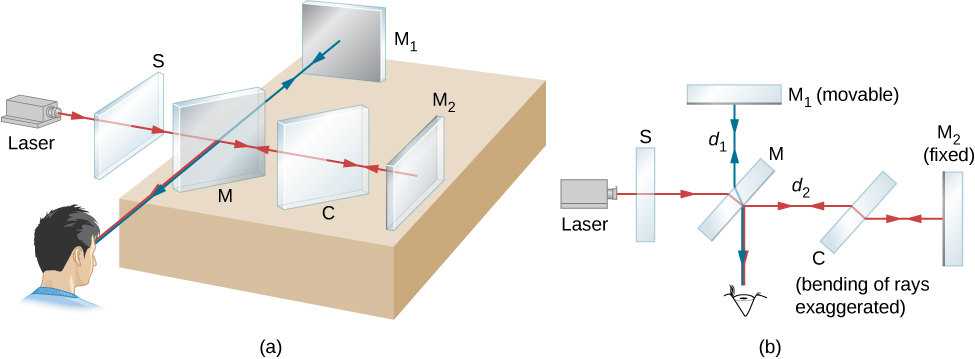
Because both beams originate from the same point on the source, they are coherent and therefore interfere. Notice from the figure that one beam passes through M three times and the other only once. To ensure that both beams traverse the same thickness of glass, a compensator plate C of transparent glass is placed in the arm containing ${\text{M}}_2$ . This plate is a duplicate of M (without the silvering) and is usually cut from the same piece of glass used to produce M. With the compensator in place, any phase difference between the two beams is due solely to the difference in the distances they travel.

The path difference of the two beams when they recombine is $2d_1-2d_2$ , where $d_1$ is the distance between M and ${\text{M}}_1$ , and $d_2$ is the distance between M and ${\text{M}}_2$ . Suppose this path difference is an integer number of wavelengths $m{\lambda }_0$ . Then, constructive interference occurs and a bright image of the point on the source is seen at the observer. Now the light from any other point on the source whose two beams have this same path difference also undergoes constructive interference and produces a bright image. The collection of these point images is a bright fringe corresponding to a path difference of $m{\lambda }_0$ ( [link] ). When ${\text{M}}_1$ is moved a distance $\text{Δ}d={\lambda }_0\text{/}2$ , this path difference changes by ${\lambda }_0$ , and each fringe moves to the position previously occupied by an adjacent fringe. Consequently, by counting the number of fringes m passing a given point as ${\text{M}}_1$ is moved, an observer can measure minute displacements that are accurate to a fraction of a wavelength, as shown by the relation