11.4 Particle accelerators and detectors  (Page 12/10)

The goal of experimental particle physics is to accurately measure elementary particles. The primary method used to achieve this end is to produce these particles in high-energy collisions and then measure the products of using highly sensitive particle detectors. These experiments are used to test and revise scientific models of particle interactions. The purpose of this section is to describe particle accelerators and detectors. Modern machines are based on earlier ones, so it is helpful to present a brief history of accelerators and detectors.

Early particle accelerators

A particle accelerator    is a machine designed to accelerate charged particles. This acceleration is usually achieved with strong electric fields, magnetic fields, or both. A simple example of a particle accelerator is the Van de Graaff accelerator (see Electric Potential ). This type of accelerator collects charges on a hollow metal sphere using a moving belt. When the electrostatic potential difference of the sphere is sufficiently large, the field is used to accelerate particles through an evacuated tube. Energies produced by a Van de Graaff accelerator are not large enough to create new particles, but the machine was important for early exploration of the atomic nucleus.

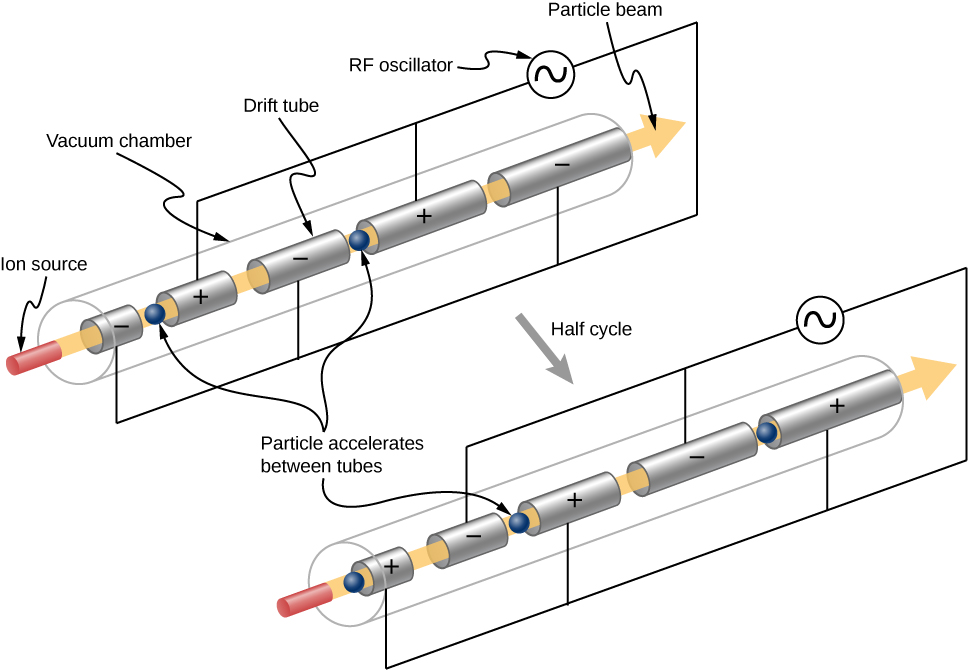
Larger energies can be produced by a linear accelerator (called a “linac”). Charged particles produced at the beginning of the linac are accelerated by a continuous line of charged hollow tubes. The voltage between a given pair of tubes is set to draw the charged particle in, and once the particle arrives, the voltage between the next pair of tubes is set to push the charged particle out. In other words, voltages are applied in such a way that the tubes deliver a series of carefully synchronized electric kicks ( [link] ). Modern linacs employ radio frequency (RF) cavities that set up oscillating electromagnetic fields, which propel the particle forward like a surfer on an ocean wave. Linacs can accelerate electrons to over 100 MeV. (Electrons with kinetic energies greater than 2 MeV are moving very close to the speed of light.) In modern particle research, linear accelerators are often used in the first stage of acceleration.