10.5 Fission  (Page 35/9)

In 1934, Enrico Fermi bombarded chemical elements with neutrons in order to create isotopes of other elements. He assumed that bombarding uranium with neutrons would make it unstable and produce a new element. Unfortunately, Fermi could not determine the products of the reaction. Several years later, Otto Hahn and Fritz Strassman reproduced these experiments and discovered that the products of these reactions were smaller nuclei. From this, they concluded that the uranium nucleus had split into two smaller nuclei.

The splitting of a nucleus is called fission    . Interestingly, U-235 fission does not always produce the same fragments. Example fission reactions include:

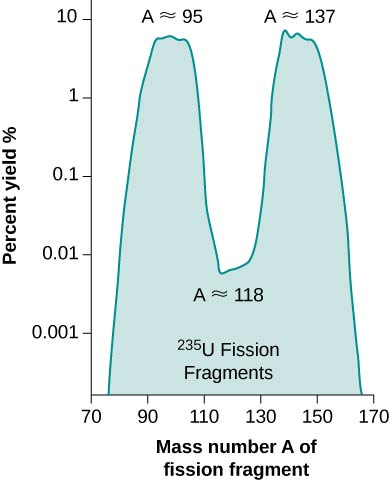
In each case, the sum of the masses of the product nuclei are less than the masses of the reactants, so the fission of uranium is an exothermic process $\left(Q>0\right).$ This is the idea behind the use of fission reactors as sources of energy ( [link] ). The energy carried away by the reaction takes the form of particles with kinetic energy. The percent yield of fragments from a U-235 fission is given in [link] .

Energy changes in a nuclear fission reaction can be understood in terms of the binding energy per nucleon curve ( [link] ). The BEN value for uranium $\left(A=236\right)$ is slightly lower than its daughter nuclei, which lie closer to the iron (Fe) peak. This means that nucleons in the nuclear fragments are more tightly bound than those in the U-235 nucleus. Therefore, a fission reaction results in a drop in the average energy of a nucleon. This energy is carried away by high-energy neutrons.

Niels Bohr and John Wheeler developed the liquid drop model    to understand the fission process. According to this model, firing a neutron at a nucleus is analogous to disturbing a droplet of water ( [link] ). The analogy works because short-range forces between nucleons in a nucleus are similar to the attractive forces between water molecules in a water droplet. In particular, forces between nucleons at the surface of the nucleus result in a surface tension similar to that of a water droplet. A neutron fired into a uranium nucleus can set the nucleus into vibration. If this vibration is violent enough, the nucleus divides into smaller nuclei and also emits two or three individual neutrons.

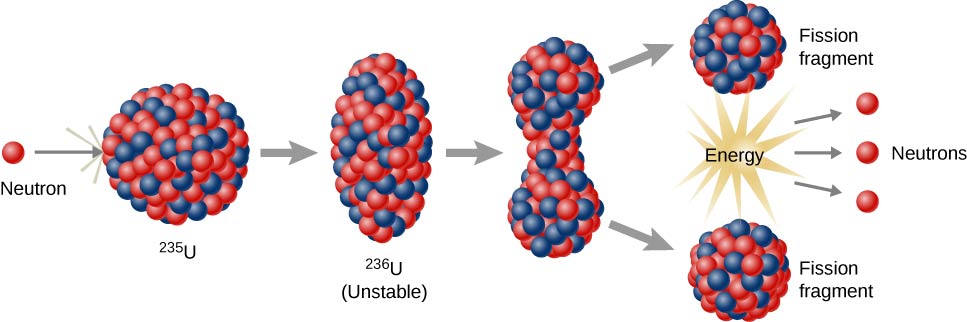
U-235 fission can produce a chain reaction . In a compound consisting of many U-235 nuclei, neutrons in the decay of one U-235 nucleus can initiate the fission of additional U-235 nuclei ( [link] ). This chain reaction can proceed in a controlled manner, as in a nuclear reactor at a power plant, or proceed uncontrollably, as in an explosion.