4.5 The carnot cycle  (Page 2/7)

This work is equal to the area enclosed by the loop shown in the pV diagram of [link] . Because the initial and final states of the system are the same, the change of the internal energy of the gas in the cycle must be zero, that is, $\text{Δ}{E}_{\text{int}}=0$ . The first law of thermodynamics then gives

and

To find the efficiency of this engine, we first divide $Q_{\text{c}}\text{by}{Q}_{\text{h}}:$

When the adiabatic constant from step 2 is divided by that of step 4, we find

Substituting this into the equation for $Q_{\text{c}}\text{/}{Q}_{\text{h}},$ we obtain

Finally, with [link] , we find that the efficiency of this ideal gas Carnot engine is given by

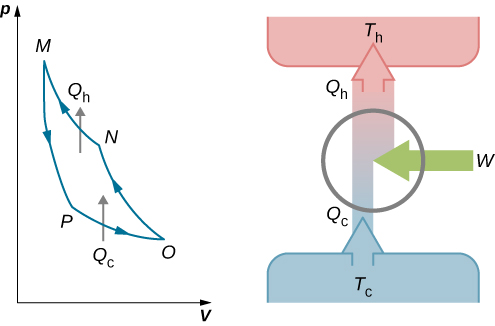
An engine does not necessarily have to follow a Carnot engine cycle. All engines, however, have the same net effect, namely the absorption of heat from a hot reservoir, the production of work, and the discarding of heat to a cold reservoir. This leads us to ask: Do all reversible cycles operating between the same two reservoirs have the same efficiency? The answer to this question comes from the second law of thermodynamics discussed earlier: All reversible engine cycles produce exactly the same efficiency . Also, as you might expect, all real engines operating between two reservoirs are less efficient than reversible engines operating between the same two reservoirs. This too is a consequence of the second law of thermodynamics shown earlier.

The cycle of an ideal gas Carnot refrigerator is represented by the pV diagram of [link] . It is a Carnot engine operating in reverse. The refrigerator extracts heat $Q_{\text{c}}$ from a cold-temperature reservoir at $T_{\text{c}}$ when the ideal gas expands isothermally. The gas is then compressed adiabatically until its temperature reaches $T_{\text{h}},$ after which an isothermal compression of the gas results in heat $Q_{\text{h}}$ being discarded to a high-temperature reservoir at $T_{\text{h}}.$ Finally, the cycle is completed by an adiabatic expansion of the gas, causing its temperature to drop to $T_{\text{c}}.$

The work done on the ideal gas is equal to the area enclosed by the path of the pV diagram. From the first law, this work is given by

An analysis just like the analysis done for the Carnot engine gives

When combined with [link] , this yields

for the coefficient of performance of the ideal-gas Carnot refrigerator. Similarly, we can work out the coefficient of performance for a Carnot heat pump as

We have just found equations representing the efficiency of a Carnot engine and the coefficient of performance of a Carnot refrigerator or a Carnot heat pump, assuming an ideal gas for the working substance in both devices. However, these equations are more general than their derivations imply. We will soon show that they are both valid no matter what the working substance is.

Carnot summarized his study of the Carnot engine and Carnot cycle into what is now known as Carnot’s principle :