| << Chapter < Page | Chapter >> Page > |
Many other processes also occur that do not fit into any of these four categories.
View this site to set up your own process in a pV diagram. See if you can calculate the values predicted by the simulation for heat, work, and change in internal energy.
When a gas expands isothermally, it does work. What is the source of energy needed to do this work?
The system must be in contact with a heat source that allows heat to flow into the system.
If the pressure and volume of a system are given, is the temperature always uniquely determined?
It is unlikely that a process can be isothermal unless it is a very slow process. Explain why. Is the same true for isobaric and isochoric processes? Explain your answer.
Isothermal processes must be slow to make sure that as heat is transferred, the temperature does not change. Even for isobaric and isochoric processes, the system must be in thermal equilibrium with slow changes of thermodynamic variables.
Two moles of a monatomic ideal gas at (5 MPa, 5 L) is expanded isothermally until the volume is doubled (step 1). Then it is cooled isochorically until the pressure is 1 MPa (step 2). The temperature drops in this process. The gas is now compressed isothermally until its volume is back to 5 L, but its pressure is now 2 MPa (step 3). Finally, the gas is heated isochorically to return to the initial state (step 4). (a) Draw the four processes in the pV plane. (b) Find the total work done by the gas.
Consider a transformation from point A to B in a two-step process. First, the pressure is lowered from 3 MPa at point A to a pressure of 1 MPa, while keeping the volume at 2 L by cooling the system. The state reached is labeled C . Then the system is heated at a constant pressure to reach a volume of 6 L in the state B . (a) Find the amount of work done on the ACB path. (b) Find the amount of heat exchanged by the system when it goes from A to B on the ACB path. (c) Compare the change in the internal energy when the AB process occurs adiabatically with the AB change through the two-step process on the ACB path.
a. 1660 J; b. −2730 J; c. It does not depend on the process.
Consider a cylinder with a movable piston containing n moles of an ideal gas. The entire apparatus is immersed in a constant temperature bath of temperature T kelvin. The piston is then pushed slowly so that the pressure of the gas changes quasi-statically from to at constant temperature T. Find the work done by the gas in terms of n, R, T, and
An ideal gas expands isothermally along AB and does 700 J of work (see below). (a) How much heat does the gas exchange along AB? (b) The gas then expands adiabatically along BC and does 400 J of work. When the gas returns to A along CA, it exhausts 100 J of heat to its surroundings. How much work is done on the gas along this path?
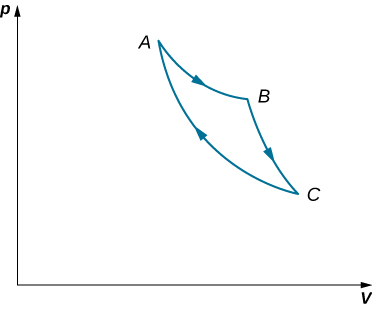
a. 700 J; b. 500 J
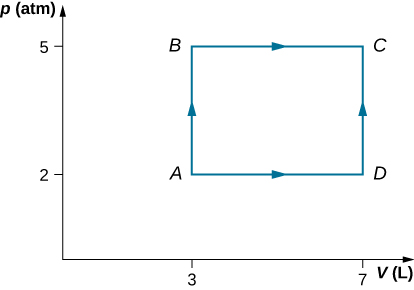
Consider the processes shown below. In the processes AB and BC, 3600 J and 2400 J of heat are added to the system, respectively. (a) Find the work done in each of the processes AB, BC, AD, and DC. (b) Find the internal energy change in processes AB and BC. (c) Find the internal energy difference between states C and A. (d) Find the total heat added in the ADC process. (e) From the information give, can you find the heat added in process AD? Why or why not?
Two moles of helium gas are placed in a cylindrical container with a piston. The gas is at room temperature and under a pressure of When the pressure from the outside is decreased while keeping the temperature the same as the room temperature, the volume of the gas doubles. (a) Find the work the external agent does on the gas in the process. (b) Find the heat exchanged by the gas and indicate whether the gas takes in or gives up heat. Assume ideal gas behavior.
a. −3 400 J; b. 3400 J enters the gas
An amount of n moles of a monatomic ideal gas in a conducting container with a movable piston is placed in a large thermal heat bath at temperature and the gas is allowed to come to equilibrium. After the equilibrium is reached, the pressure on the piston is lowered so that the gas expands at constant temperature. The process is continued quasi-statically until the final pressure is 4/3 of the initial pressure (a) Find the change in the internal energy of the gas. (b) Find the work done by the gas. (c) Find the heat exchanged by the gas, and indicate, whether the gas takes in or gives up heat.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?