3.4 Thermodynamic processes  (Page 2/11)

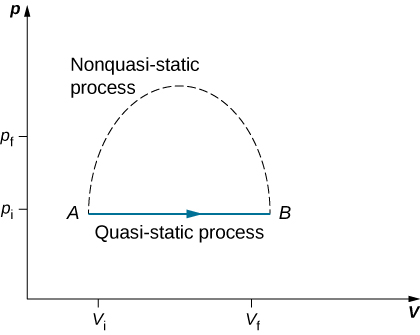
Since quasi-static processes cannot be completely realized for any finite change of the system, all processes in nature are non-quasi-static. Examples of quasi-static and non-quasi-static processes are shown in [link] . Despite the fact that all finite changes must occur essentially non-quasi-statically at some stage of the change, we can imagine performing infinitely many quasi-static process corresponding to every quasi-static process. Since quasi-static processes can be analyzed analytically, we mostly study quasi-static processes in this book. We have already seen that in a quasi-static process the work by a gas is given by pdV .

Isothermal processes

An isothermal process    is a change in the state of the system at a constant temperature. This process is accomplished by keeping the system in thermal equilibrium with a large heat bath during the process. Recall that a heat bath is an idealized “infinitely” large system whose temperature does not change. In practice, the temperature of a finite bath is controlled by either adding or removing a finite amount of energy as the case may be.

As an illustration of an isothermal process, consider a cylinder of gas with a movable piston immersed in a large water tank whose temperature is maintained constant. Since the piston is freely movable, the pressure inside $P_{\text{in}}$ is balanced by the pressure outside $P_{\text{out}}$ by some weights on the piston, as in [link] .

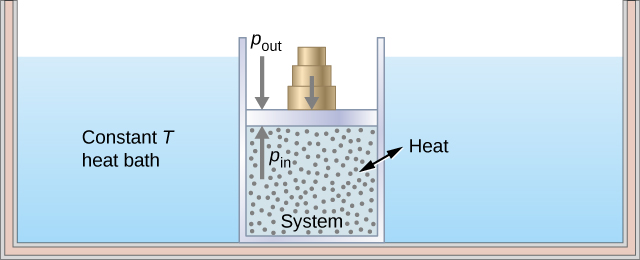
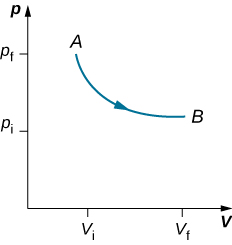
As weights on the piston are removed, an imbalance of forces on the piston develops. The net nonzero force on the piston would cause the piston to accelerate, resulting in an increase in volume. The expansion of the gas cools the gas to a lower temperature, which makes it possible for the heat to enter from the heat bath into the system until the temperature of the gas is reset to the temperature of the heat bath. If weights are removed in infinitesimal steps, the pressure in the system decreases infinitesimally slowly. This way, an isothermal process can be conducted quasi-statically. An isothermal line on a ( p , V ) diagram is represented by a curved line from starting point A to finishing point B , as seen in [link] . For an ideal gas, an isothermal process is hyperbolic, since for an ideal gas at constant temperature, $p\propto \frac{1}{V}$ .