| << Chapter < Page | Chapter >> Page > |
The expansion is isothermal, so T remains constant over the entire process. Since n and R are also constant, the only variable in the integrand is V , so the work done by an ideal gas in an isothermal process is
Notice that if (expansion), W is positive, as expected.
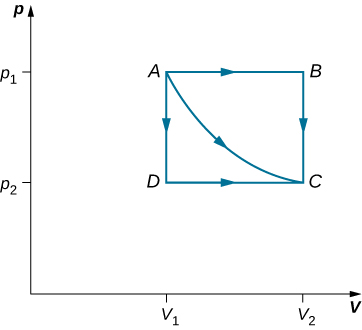
The straight lines from A to B and then from B to C represent a different process. Here, a gas at a pressure first expands isobarically (constant pressure) and quasi-statically from , after which it cools quasi-statically at the constant volume until its pressure drops to . From A to B , the pressure is constant at p , so the work over this part of the path is
From B to C , there is no change in volume and therefore no work is done. The net work over the path ABC is then
A comparison of the expressions for the work done by the gas in the two processes of [link] shows that they are quite different. This illustrates a very important property of thermodynamic work: It is path dependent . We cannot determine the work done by a system as it goes from one equilibrium state to another unless we know its thermodynamic path. Different values of the work are associated with different paths.
where a and b are two parameters for a specific gas. Suppose the gas expands isothermally and quasi-statically from volume to volume How much work is done by the gas during the expansion?
Because T is constant under the isothermal condition, the work done by 1 mol of a van der Waals gas in expanding from a volume to a volume is thus
Check Your Understanding How much work is done by the gas, as given in [link] , when it expands quasi-statically along the path ADC ?
The internal energy of a thermodynamic system is, by definition, the sum of the mechanical energies of all the molecules or entities in the system. If the kinetic and potential energies of molecule i are and respectively, then the internal energy of the system is the average of the total mechanical energy of all the entities:

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?