14.4 Rl circuits  (Page 7/4)

A circuit with resistance and self-inductance is known as an RL circuit. [link] (a) shows an RL circuit consisting of a resistor, an inductor, a constant source of emf, and switches ${\text{S}}_1$ and ${\text{S}}_2.$ When ${\text{S}}_1$ is closed, the circuit is equivalent to a single-loop circuit consisting of a resistor and an inductor connected across a source of emf ( [link] (b)). When ${\text{S}}_1$ is opened and ${\text{S}}_2$ is closed, the circuit becomes a single-loop circuit with only a resistor and an inductor ( [link] (c)).

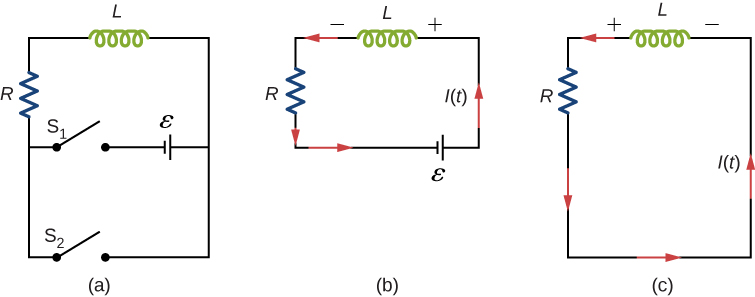
We first consider the RL circuit of [link] (b). Once ${\text{S}}_1$ is closed and ${\text{S}}_2$ is open, the source of emf produces a current in the circuit. If there were no self-inductance in the circuit, the current would rise immediately to a steady value of $\text{ε}\text{/}R.$ However, from Faraday’s law, the increasing current produces an emf $V_L=\text{−}L(dI\text{/}dt)$ across the inductor. In accordance with Lenz’s law, the induced emf counteracts the increase in the current and is directed as shown in the figure. As a result, I(t) starts at zero and increases asymptotically to its final value.

Applying Kirchhoff’s loop rule to this circuit, we obtain

which is a first-order differential equation for I(t) . Notice its similarity to the equation for a capacitor and resistor in series (See RC Circuits ). Similarly, the solution to [link] can be found by making substitutions in the equations relating the capacitor to the inductor. This gives

where

is the inductive time constant    of the circuit.

The current I(t) is plotted in [link] (a). It starts at zero, and as $t\to \infty$ , I(t) approaches $\text{ε}\text{/}R$ asymptotically. The induced emf $V_L(t)$ is directly proportional to dI / dt , or the slope of the curve. Hence, while at its greatest immediately after the switches are thrown, the induced emf decreases to zero with time as the current approaches its final value of $\text{ε}\text{/}R.$ The circuit then becomes equivalent to a resistor connected across a source of emf.

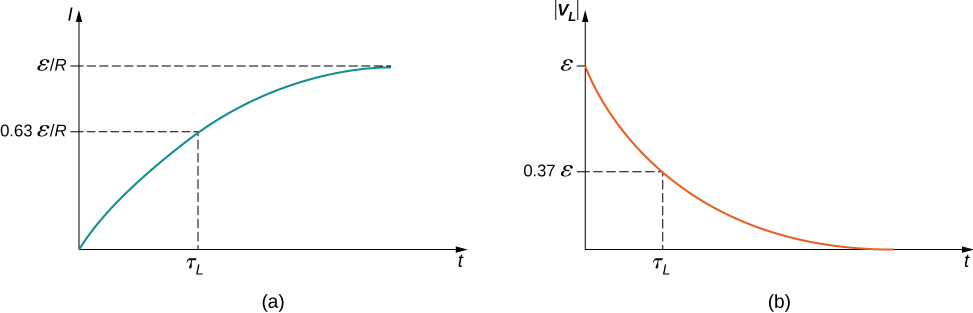
The energy stored in the magnetic field of an inductor is

Thus, as the current approaches the maximum current $\epsilon \text{/}R$ , the stored energy in the inductor increases from zero and asymptotically approaches a maximum of $L{(\epsilon \text{/}R)}^2\text{/}2.$

The time constant ${\tau }_L$ tells us how rapidly the current increases to its final value. At $t={\tau }_L,$ the current in the circuit is, from [link] ,

which is $63\text{\%}$ of the final value $\text{ε}\text{/}R$ . The smaller the inductive time constant ${\tau }_L=L\text{/}R,$ the more rapidly the current approaches $\text{ε}\text{/}R$ .

We can find the time dependence of the induced voltage across the inductor in this circuit by using $V_L(t)=\text{−}L(dI\text{/}dt)$ and [link] :

The magnitude of this function is plotted in [link] (b). The greatest value of $L\left(dI\text{/}dt\right)\text{is}\epsilon ;$ it occurs when dI/dt is greatest, which is immediately after ${\text{S}}_1$ is closed and ${\text{S}}_2$ is opened. In the approach to steady state, dI/dt decreases to zero. As a result, the voltage across the inductor also vanishes as $t\to \infty .$