| << Chapter < Page | Chapter >> Page > |
In 1879, E.H. Hall devised an experiment that can be used to identify the sign of the predominant charge carriers in a conducting material. From a historical perspective, this experiment was the first to demonstrate that the charge carriers in most metals are negative.
Visit this website to find more information about the Hall effect.
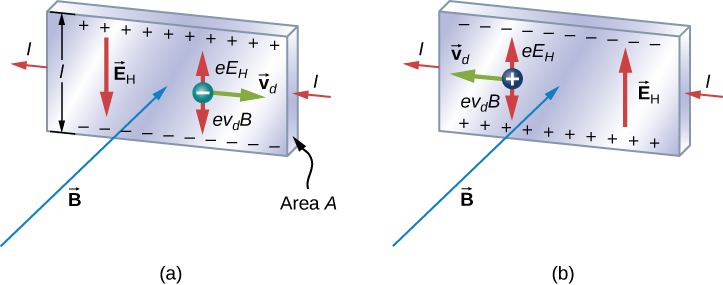
We investigate the Hall effect by studying the motion of the free electrons along a metallic strip of width l in a constant magnetic field ( [link] ). The electrons are moving from left to right, so the magnetic force they experience pushes them to the bottom edge of the strip. This leaves an excess of positive charge at the top edge of the strip, resulting in an electric field E directed from top to bottom. The charge concentration at both edges builds up until the electric force on the electrons in one direction is balanced by the magnetic force on them in the opposite direction. Equilibrium is reached when:
where e is the magnitude of the electron charge, vd is the drift speed of the electrons, and E is the magnitude of the electric field created by the separated charge. Solving this for the drift speed results in
A scenario where the electric and magnetic fields are perpendicular to one another is called a crossed-field situation. If these fields produce equal and opposite forces on a charged particle with the velocity that equates the forces, these particles are able to pass through an apparatus, called a velocity selector , undeflected. This velocity is represented in [link] . Any other velocity of a charged particle sent into the same fields would be deflected by the magnetic force or electric force.
Going back to the Hall effect, if the current in the strip is I , then from Current and Resistance , we know that
where n is the number of charge carriers per volume and A is the cross-sectional area of the strip. Combining the equations for vd and I results in
The field E is related to the potential difference V between the edges of the strip by
The quantity V is called the Hall potential and can be measured with a voltmeter. Finally, combining the equations for I and E gives us
where the upper edge of the strip in [link] is positive with respect to the lower edge.
We can also combine [link] and [link] to get an expression for the Hall voltage in terms of the magnetic field:
What if the charge carriers are positive, as in [link] ? For the same current I , the magnitude of V is still given by [link] . However, the upper edge is now negative with respect to the lower edge. Therefore, by simply measuring the sign of V , we can determine the sign of the majority charge carriers in a metal.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?