| << Chapter < Page | Chapter >> Page > |
In chapters [link] and [link] the so-called wave-particle duality of light is described. This duality states that light displays properties of both waves and of particles, depending on the experiment performed. For example, interference and diffraction of light are properties of its wave nature, while the photoelectric effect is a property of its particle nature. In fact we call a particle of light a photon.
Hopefully you have realised that nature loves symmetry. So, if light which was originally believed to be a wave also has a particle nature, then perhaps particles, also display a wave nature. In other words matter which we originally thought of as particles may also display a wave-particle duality.
Einstein showed that for a photon, its momentum, , is equal to its energy, divided by the speed of light, :
The energy of the photon can also be expressed in terms of the wavelength of the light, :
where is Planck's constant. Combining these two equations we find that the the momentum of the photon is related to its wavelength
or equivalently
In 1923, Louis de Broglie proposed that this equation not only holds for photons, but also holds for particles of matter. This is known as the de Broglie hypothesis.
A particle of mass moving with velocity has a wavelength related to is momentum by
This wavelength, , is known as the de Broglie wavelength of the particle (where is Planck's constant).
Since the value of Planck's constant is incredibly small , the wavelike nature of everyday objects is not really observable.
The de Broglie hypothesis was proposed by French physicist Louis de Broglie (15 August 1892 – 19 March 1987) in 1923 in his PhD thesis. He was awarded the Nobel Prize for Physics in 1929 for this work, which made him the first person to receive a Nobel Prize on a PhD thesis.
A cricket ball has a mass of and is bowled towards a bowler at . Calculate the de Broglie wavelength of the cricket ball?
We are required to calculate the de Broglie wavelength of a cricket ball given its mass and speed. We can do this by using:
We are given:
and we know:
This wavelength is considerably smaller than the diameter of a proton which is approximately . Hence the wave-like properties of this cricket ball are too small to be observed.
Calculate the de Broglie wavelength of an electron moving at 40 m s .
We are required to calculate the de Broglie wavelength of an electron given its speed. We can do this by using:
We are given:
and we know:
Although the electron and cricket ball in the two previous examples are travelling at the same velocity the de Broglie wavelength of the electron is much larger than that of the cricket ball. This is because the wavelength is inversely proportional to the mass of the particle.
Calculate the de Broglie wavelength of a electron moving at . ( of the speed of light.)
We are required to calculate the de Broglie wavelength of an electron given its speed. We can do this by using:
We are given:
and we know:
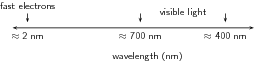
This is the size of an atom. For this reason, electrons moving at high velocities can be used to “probe" the structure of atoms. This is discussed in more detail at the end of this chapter. [link] compares the wavelengths of fast moving electrons to the wavelengths of visible light.
Since the de Broglie wavelength of a particle is inversely proportional to its velocity, the wavelength decreases as the velocity increases. This is confirmed in the last two examples with the electrons. De Broglie's hypothesis was confirmed by Davisson and Germer in 1927 when they observed a beam of electrons being diffracted off a nickel surface. The diffraction means that the moving electrons have a wave nature. They were also able to determine the wavelength of the electrons from the diffraction. To measure a wavelength one needs two or more diffracting centres such as pinholes, slits or atoms. For diffraction to occur the centres must be separated by a distance about the same size as the wavelength. Theoretically, all objects, not just sub-atomic particles, exhibit wave properties according to the de Broglie hypothesis.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 physical science' conversation and receive update notifications?