Vertical projectile motion  (Page 15/3)

Introduction

In Grade 10, we studied motion in one dimension and briefly looked at vertical motion. In this chapter we will discuss vertical motion and also look at motion in two dimensions. In Grade 11, we studied the conservation of momentum and looked at applications in one dimension. In this chapter we will look at momentum in two dimensions.

Vertical projectile motion

In Grade 10, we studied the motion of objects in free fall and we saw that an object in free fall falls with gravitational acceleration $g$ . Now we can consider the motion of objects that are thrown upwards and then fall back to the Earth. We call this projectile motion and we will only consider the situation where the object is thrown straight upwards and then falls straight downwards - this means that there is no horizontal displacement of the object, only a vertical displacement.

Motion in a gravitational field

When an object is in the earth's gravitational field, it always accelerates downwards, towards the centre of the earth, with a constant acceleration $g$ , no matter whether the object is moving upwards or downwards. This is shown in [link] .

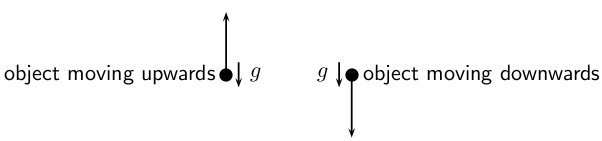
This means that if an object is moving upwards, its velocity decreases until it stops ( $v_f=0$  m $·$ s ${}^{-1}$ ). This is the maximum height that the object reaches, because after this, the object starts to fall.

Consider an object thrown upwards from a vertical height $h_o$ . We have seen that the object will travel upwards with decreasing velocity until it stops, at which point it starts falling. The time that it takes for the object to fall down to height $h_o$ is the same as the time taken for the object to reach its maximum height from height $h_o$ .

Equations of motion

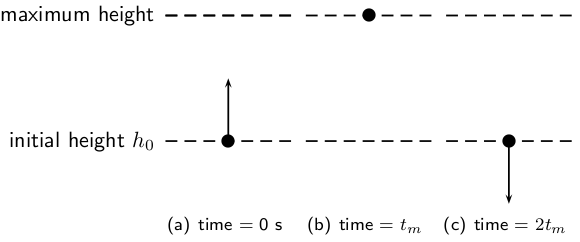
The equations of motion that were used in Chapter  [link] to describe free fall can be used for projectile motion. These equations are the same as those equations that were derived in Chapter  [link] , but with acceleration from gravity: $a=g$ . We use $g=9,8\mathrm{m}·{\mathrm{s}}^{-2}$ for our calculations.

Remember that when you use these equations, you are dealing with vectors which have magnitude and direction. Therefore, you need to decide which direction will be the positive direction so that your vectors have the correct signs.