Capacitive and inductive circuits  (Page 21/4)

Introduction

Electronics and electrical devices surround us in daily life. From the street lights and water pumps to computers and digital phones, electronics have enabled the digital revolution to occur. All electronics are built on a backbone of simple circuits, and so an understanding of circuits is vital in understanding more complex devices.

This chapter will explain the basic physics principles of many of the components of electronic devices. We will begin with an explanation of capacitors and inductors. We see how these are used in tuning a radio. Next, we look at active components such as transistors and operational amplifiers. Lastly, the chapter will finish with an explanation of digital electronics, including logic gates and counting circuits.

Before studying this chapter, you will want to remind yourself of:

1. The meaning of voltage ( $V$ ), current ( $I$ ) and resistance ( $R$ ), as covered in Grade 10, and Grade 11.
2. Capacitors in electric circuits, as covered in Grade 11 (see section 17.6).
3. Semiconductors, as covered in Grade 11 (see chapter 20).
4. The meaning of an alternating current (see section 28.3).
5. Capacitance ( $C$ ) and Inductance ( $L$ ) (see section 28.4).

Capacitive and inductive circuits

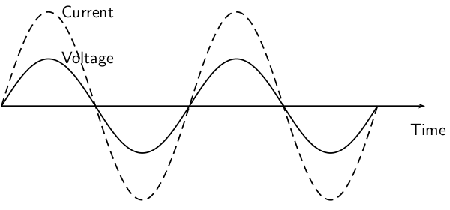
Earlier in Grade 12, you were shown alternating currents (AC) and you saw that the voltage and the current varied with time. If the AC supply is connected to a resistor, then the current and voltage will be proportional to each other. This means that the current and voltage will `peak' at the same time. We say that the current and voltage are in phase . This is shown in [link] .

When a capacitor is connected to an alternating voltage, the maximum voltage is proportional to the maximum current, but the maximum voltage does not occur at the same time as the maximum current. The current has its maximum (it peaks) one quarter of a cycle before the voltage peaks. Engineers say that the `current leads the voltage by ${90}^{\circ }$ '. This is shown in [link] .

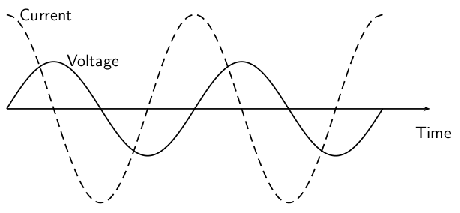
For a circuit with a capacitor, the instantaneous value of $\frac{V}{I}$ is not constant. However, the value of $\frac{V_{max}}{I_{max}}$ is useful, and is called the capacitive reactance ( $X_C$ ) of the component. Because it is still a voltage divided by a current (like resistance), its unit is the ohm. The value of $X_C$ ( $C$ standing for capacitor) depends on its capacitance ( $C$ ) and the frequency ( $f$ ) of the alternating current (in South Africa 50 Hz).

$X_C=\frac{V_{max}}{I_{max}}=\frac{1}{2\pi fC}$

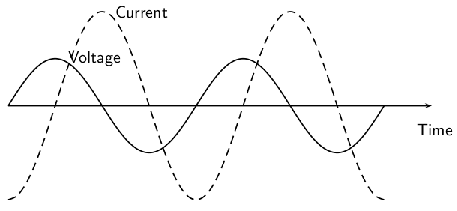
Inductors are very similar, but the current peaks ${90}^{\circ }$ after the voltage. This is shown in [link] . Engineers say that the `current lags the voltage'. Again, the ratio of maximum voltage to maximum current is called the reactance — this time inductive reactance ( $X_L$ ). The value of the reactance depends on its inductance ( $L$ ).

$X_L=\frac{V_{max}}{I_{max}}=2\pi fL$