| << Chapter < Page | Chapter >> Page > |
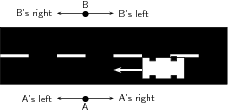
Consider two people standing, facing each other on either side of a road. A car drives past them, heading West. For the person facing South, the car was moving toward the right. However, for the person facing North, the car was moving toward the left. This discrepancy is due to the fact that the two people used two different frames of reference from which to investigate this system. If each person were asked in what direction the car were moving, they would give a different answer. The answer would be relative to their frame of reference.
A frame of reference is the point of view from which a system is observed.
In practical terms, a frame of reference is a set of axes (specifying directions) with an origin. An observer can then measure the position and motion of all points in a system, as well as the orientation of objects in the system relative to the frame of reference.
There are two types of reference frames: inertial and non-inertial. An inertial frame of reference travels at a constant velocity, which means that Newton's first law (inertia) holds true. A non-inertial frame of reference, such as a moving car or a rotating carousel, accelerates. Therefore, Newton's first law does not hold true in a non-inertial reference frame, as objects appear to accelerate without the appropriate forces.
Frames of reference are important because (as we have seen in the introductory example) the velocity of a car can differ depending on which frame of reference is used.
Frames of reference are especially important in special relativity, because when a frame of reference is moving at some significant fraction of the speed of light, then the flow of time in that frame does not necessarily apply in another reference frame. The speed of light is considered to be the only true constant between moving frames of reference.
The next worked example will explain this.
The velocity of an object is frame dependent. More specifically, the perceived velocity of an object depends on the velocity of the observer. For example, a person standing on shore would observe the velocity of a boat to be different than a passenger on the boat.
The speedometer of a motor boat reads 5 m s . The boat is moving East across a river which has a current traveling 3 m s North. What would the velocity of the motor boat be according to an observer on the shore?

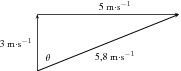
The observer on the shore sees the boat moving with a velocity of 5,8 m s at 59,04 east of north due to the current pushing the boat perpendicular to its velocity. This is contrary to the perspective of a passenger on the boat who perceives the velocity of the boat to be 5 m s due East. Both perspectives are correct as long as the frame of the observer is considered.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 physical science' conversation and receive update notifications?