| << Chapter < Page | Chapter >> Page > |
| Inputs | Output | |
| A | B | |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
This device is called an AND gate, because the output is only 1 if one input AND the other input are both 1.
When we use logic gates we use the low voltage state 0 to represent `false'. The high voltage state 1 represents `true'. This is why the word AND is so appropriate. A AND B is true (1) if, and only if, A is true (1) AND B is true (1).
Sometimes, the AND operation is written as multiplication. A AND B is written AB. If either A or B are 0, then AB will also be 0. For AB to be 1, we need A and B to both be 1. Multiplication of the numbers 0 and 1 does exactly the same job as an AND gate.
Problem: You build the circuit for the airliner toilets using an AND gate. Your customer is pleased, but she says that it would be better if the display lit up when there was a free toilet. In other words, the display should light up unless both toilets are in use. To do this we want a circuit which does the opposite of an AND gate. We want a circuit which would give the output 0 where an AND gate would give 1. We want a circuit which would give the output 1 where an AND gate would give 0. This circuit is called a NAND gate.
The symbol for the NAND gate is:
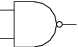
The truth table for the NAND gate is shown below.
| Inputs | Output | |
| A | B | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
You may have noticed that we could have done this job on the airliner by using our earlier circuit, with a NOT gate added between the original AND gate and the display. This is where the word NAND comes from — it is short for NotAND.
Problem: A long, dark corridor has two light switches — one at each end of the corridor. The switches each send an output of 0 to the control unit if no-one has pressed the switch. If someone presses the switch, its output is 1. The lights in the corridor should come on if either switch is pressed. To do this job, the control unit needs an OR gate. The symbol for the OR gate is:
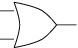
The truth table for the OR gate is shown.
| Inputs | Output | |
| A | B | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
You can see that the output is 1 (and the lights come on in the corridor) if either one switch OR the other is pressed. Pressing both switches also turns on the lights, as the last row in the table shows.
Sometimes you will see A OR B written mathematically as A+B. This makes sense, since if A=0 and B=0, then A OR B = A+B = 0. Similarly, if A=0 and B=1, then A OR B = A+B = 1. If A=1 and B=0, then A OR B = A+B = 1 once again. The only case where the OR function differs from normal addition is when A=1 and B=1. Here A OR B = 1 in logic, but A+B=2 in arithmetic. However, there is no such thing as `2' in logic, so we define + to mean `OR', and write 1+1=1 with impunity!
If you wish, you can prove that the normal rules of algebra still work using this notation: A+(B+C) = (A+B)+C, A(BC) = (AB)C, and A(B+C) = AB + AC. This special kind of algebra where variables can only be 0 (representing false) or 1 (representing true) is called Boolean algebra.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 physical science' conversation and receive update notifications?