Standing waves in string instruments  (Page 15/2)

Introduction

What is your favorite musical instrument? How do you play it? Do you pluck a string, like a guitar? Do you blow through it, like a flute? Do you hit it, like a drum?All musical instruments work by making standing waves. Each instrument has a unique sound because of the special waves made in it. These waves could be in the strings of a guitar or violin.They could also be in the skin of a drum or a tube of air in a trumpet. These waves are picked up by the air and later reach your ear as sound.

In Grade 10, you learned about standing waves and boundary conditions. We saw a rope that was:

• fixed at both ends
• fixed at one end and free at the other

We also saw a pipe that was:

• closed at both ends
• open at both ends
• open at one end, closed at the other

String and wind instruments are good examples of standing waves on strings and pipes.

One way to describe standing waves is to count nodes. Recall that a node is a point on a string that does not move as the wave changes.The anti-nodes are the highest and lowest points on the wave. There is a node at each end of a fixed string. There is also a node at the closed end of a pipe.But an open end of a pipe has an anti-node.

What causes a standing wave? There are incident and reflected waves traveling back and forth on our string or pipe. For some frequencies, these waves combine in just the right way so that the whole wave appears to be standing still.These special cases are called harmonic frequencies, or harmonics . They depend on the length and material of the medium.

Harmonic

A harmonic frequency is a frequency at which standing waves can be made in a particular object or on a particular instrument.

Standing waves in string instruments

Let us look at a basic "instrument": a string pulled tight and fixed at both ends. When you pluck the string, you hear a certain pitch. This pitch is made by a certain frequency.What causes the string to emit sounds at this pitch?

You have learned that the frequency of a standing wave depends on the length of the wave. The wavelength depends on the nodes and anti-nodes.The longest wave that can "fit" on the string is shown in [link] . This is called the fundamental or natural frequency of the string. The string has nodes at both ends. The wavelength of the fundamental is twice the length of the string.

Now put your finger on the center of the string. Hold it down gently and pluck it. The standing wave now has a node in the middle of the string. There are three nodes.We can fit a whole wave between the ends of the string. This means the wavelength is equal to the length of the string.This wave is called the first harmonic. As we add more nodes, we find the second harmonic, third harmonic, and so on.We must keep the nodes equally spaced or we will lose our standing wave.

Investigation : waves on a string fixed at both ends

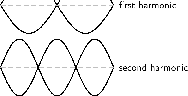
This chart shows various waves on a string. The string length $L$ is the dashed line.

1. Fill in the:
   • number of nodes
   • number of anti-nodes
   • wavelength in terms of $L$
   The first and last waves are done for you.

   Wave	Nodes	Antinodes	Wavelength

2. Use the chart to find a formula for the wavelength in terms of the number of nodes.