Coulomb's law  (Page 2/2)

1. Determine what is required

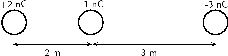
   We are needed to calculate the net force on $Q_2$ . This force is the sum of the two electrostatic forces - the forces between $Q_1$ on $Q_2$ and $Q_3$ on $Q_2$ .

2. Determine how to approach the problem
   • We need to calculate the two electrostatic forces on $Q_2$ , using Coulomb's Law.
   • We then need to add up the two forces using our rules for adding vector quantities, because force is a vector quantity.
3. Determine what is given

   We are given all the charges and all the distances.

4. Calculate the forces.

   Force of $Q_1$ on $Q_2$ :

   $$\begin{array}{ccc}\hfill F& =& k\frac{Q_1{Q}_2}{r^2}\hfill \\ & =& (8,99\times {10}^9)\frac{(2\times {10}^{-9})(1\times {10}^{-9})}{(2\times {10}^{-4})}\hfill \\ & =& 4,5\times {10}^{-5}\mathrm{N}\hfill \end{array}$$

   Force of $Q_3$ on $Q_2$ :

   $$\begin{array}{ccc}\hfill F& =& k\frac{Q_2{Q}_3}{r^2}\hfill \\ & =& (8,99\times {10}^9)\frac{(1\times {10}^{-9})(3\times {10}^{-9})}{(4\times {10}^{-4}}\hfill \\ & =& 1,69\times {10}^{-5}\mathrm{N}\hfill \end{array}$$

   Both forces act in the same direction because the force between $Q_1$ and $Q_2$ is repulsive (like charges) and the force between $Q_2$ and $Q_3$ is attractive (unlike charges).

   Therefore,

   $$\begin{array}{ccc}\hfill F_{tot}& =& 4,50\times {10}^{-5}+4,50\times {10}^{-5}\hfill \\ & =& 6,19\times {10}^{-5}\mathrm{N}\hfill \end{array}$$

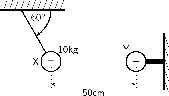
How are we going to determine the charge on X? Well, if we know the force between X and Y we can use Coulomb's Law to determinetheir charges as we know the distance between them. So, firstly, we need to determine the magnitude of the electrostatic forcebetween X and Y.

1. Is everything in S.I. units? The distance between X and Y is $50\mathrm{cm}=0,5\mathrm{m}$ , and the mass of X is 10kg.

2. Draw a force diagram

   Draw the forces on X (with directions) and label.

   

3. Calculate the magnitude of the electrostatic force, $F_E$

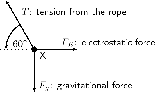
   Since nothing is moving (system is in equilibrium) the vertical and horizontal components of the gravitational force must cancel the vertical and horizontal components of the electrostatic force. Thus

   $$\begin{array}{c}\hfill F_E=Tcos\left({60}^{\circ }\right);F_g=Tsin\left({60}^{\circ }\right).\end{array}$$

   The only force we know is the gravitational force $F_g=mg$ . Now we can calculate the magnitude of $T$ from above:

   $$\begin{array}{c}\hfill T=\frac{F_g}{sin\left({60}^{\circ }\right)}=\frac{\left(10\right)\left(10\right)}{sin\left({60}^{\circ }\right)}=115,5\mathrm{N}.\end{array}$$

   Which means that $F_E$ is:

   $$F_E=Tcos\left({60}^{\circ }\right)=115,5·cos\left({60}^{\circ }\right)=57,75\mathrm{N}$$

4. Now that we know the magnitude of the electrostatic force between X and Y, we can calculate their charges usingCoulomb's Law. Don't forget that the magnitudes of the charges on X and Y are the same: $Q_{\mathrm{X}}=Q_{\mathrm{Y}}$ . The magnitude of the electrostatic force is

   $$\begin{array}{ccc}\hfill F_E& =& k\frac{Q_{\mathrm{X}}{Q}_{\mathrm{Y}}}{r^2}=k\frac{Q_{\mathrm{X}}^2}{r^2}\hfill \\ \hfill Q_{\mathrm{X}}& =& \sqrt{\frac{F_E{r}^2}{k}}\hfill \\ & =& \sqrt{\frac{(57.75){(0.5)}^2}{8.99\times {10}^9}}\hfill \\ & =& 5.66\times {10}^{-5}\mathrm{C}\hfill \end{array}$$

   Thus the charge on X is $-5.66\times {10}^{-5}\mathrm{C}$ .