11.13 Torque and levers  (Page 23/3)

Torque and levers

Torque

This chapter has dealt with forces and how they lead to motion in a straight line. In this section, we examine how forces lead to rotational motion.

When an object is fixed or supported at one point and a force acts on it a distance away from the support, it tends to make the object turn. The moment of force or torque (symbol, $\tau$ read tau ) is defined as the product of the distance from the support or pivot ( $r$ ) and the component of force perpendicular to the object, $F_{\perp }$ .

Torque can be seen as a rotational force. The unit of torque is N $·$ m and torque is a vector quantity. Some examples of where torque arises are shown in Figures  [link] , [link] and [link] .

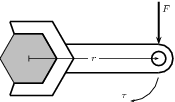
For example in [link] , if a force $F$ of 10 N is applied perpendicularly to the spanner at a distance $r$ of 0,3 m from the center of the bolt, then the torque applied to the bolt is:

If the force of 10 N is now applied at a distance of 0,15 m from the centre of the bolt, then the torque is:

This shows that there is less torque when the force is applied closer to the bolt than further away.

If you are trying to loosen (or tighten) a bolt, apply the force on the spanner further away from the bolt, as this results in a greater torque to the bolt making it easier to loosen.

The direction of a torque is either clockwise or anticlockwise. When torques are added, choose one direction as positive and the opposite direction as negative. If equal clockwise and anticlockwise torques are applied to an object, they will cancel out and there will be no net turning effect.

Several children are playing in the park. One child pushes the merry-go-round with a force of 50 N. The diameter of the merry-go-round is 3,0 m. What torque does the child apply if the force is applied perpendicularly at point A?

1. Identify what has been given

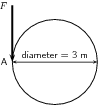
   The following has been given:

   • the force applied, $F$  = 50 N
   • the diameter of the merry-go-round, $2r$  = 3 m, therefore $r$  = 1,5 m.

   The quantities are in SI units.

2. Decide how to approach the problem

   We are required to determine the torque applied to the merry-go-round. We can do this by using:

   $$\tau =F_{\perp }·r$$

   We are given $F_{\perp }$ and we are given the diameter of the merry-go-round. Therefore, $r$ = 1,5 m.

3. Solve the problem
   $$\begin{array}{ccc}\hfill \tau & =& F_{\perp }·r\hfill \\ & =& \left(50\mathrm{N}\right)(1,5\mathrm{m})\hfill \\ & =& 75\mathrm{N}·\mathrm{m}\hfill \end{array}$$
4. Write the final answer

   75  $\mathrm{N}·\mathrm{m}$ of torque is applied to the merry-go-round.

Got questions? Get instant answers now!

Kevin is helping his dad replace the flat tyre on the car. Kevin has been asked to undo all the wheel nuts. Kevin holds the spanner at the same distance for all nuts, but applies the force at two angles (90 ${}^{\circ }$ and 60 ${}^{\circ }$ ). If Kevin applies a force of 60 N, at a distance of 0,3 m away from the nut, which angle is the best to use? Prove your answer by means of calculations.

1. Identify what has been given

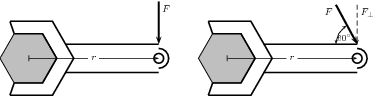
   The following has been given:

   • the force applied, $F$  = 60 N
   • the angles at which the force is applied, $\theta ={90}^{\circ }$ and $\theta ={60}^{\circ }$
   • the distance from the centre of the nut at which the force is applied, $r$  = 0,3 m

   The quantities are in SI units.

2. Decide how to approach the problem

   We are required to determine which angle is more better to use. This means that we must find which angle gives the higher torque. We can use

   $$\tau =F_{\perp }·r$$

   to determine the torque. We are given $F$ for each situation. $F_{\perp }=Fsin\theta$ and we are given $\theta$ . We are also given the distance away from the nut, at which the force is applied.

3. Solve the problem for $\theta ={90}^{\circ }$

   $F_{\perp }=F$

   $$\begin{array}{ccc}\hfill \tau & =& F_{\perp }·r\hfill \\ & =& \left(60\mathrm{N}\right)(0,3\mathrm{m})\hfill \\ & =& 18\mathrm{N}·\mathrm{m}\hfill \end{array}$$
4. Solve the problem for $\theta ={60}^{\circ }$
   $$\begin{array}{ccc}\hfill \tau & =& F_{\perp }·r\hfill \\ & =& Fsin\theta ·r\hfill \\ & =& \left(60\mathrm{N}\right)sin\left(\theta \right)(0,3\mathrm{m})\hfill \\ & =& 15,6\mathrm{N}·\mathrm{m}\hfill \end{array}$$
5. Write the final answer

   The torque from the perpendicular force is greater than the torque from the force applied at ${60}^{\circ }$ . Therefore, the best angle is ${90}^{\circ }$ .

Got questions? Get instant answers now!