| << Chapter < Page | Chapter >> Page > |
Vectors are mathematical objects and we need to understand the mathematical properties of vectors, like adding and subtracting.
For all the examples in this section, we will use displacement as our vector quantity. Displacement was discussed in Grade 10.
Displacement is defined as the distance together with direction of the straight line joining a final point to an initial point.
Remember that displacement is just one example of a vector. We could just as well have decided to use forces or velocities to illustrate the properties of vectors.
When vectors are added, we need to add both a magnitude and a direction. For example, take 2 steps in the forward direction, stop and then take another 3 steps in the forward direction. The first 2 steps is a displacement vector and the second 3 steps is also a displacement vector. If we did not stop after the first 2 steps, we would have taken 5 steps in the forward direction in total. Therefore, if we add the displacement vectors for 2 steps and 3 steps, we should get a total of 5 steps in the forward direction. Graphically, this can be seen by first following the first vector two steps forward and then following the second one three steps forward (ie. in the same direction):

We add the second vector at the end of the first vector, since this is where we now are after the first vector has acted. The vector from the tail of the first vector (the starting point) to the head of the last (the endpoint) is then the sum of the vectors. This is the head-to-tail method of vector addition.
As you can convince yourself, the order in which you add vectors does not matter. In the example above, if you decided to first go 3 stepsforward and then another 2 steps forward, the end result would still be 5 steps forward.
The final answer when adding vectors is called the resultant . The resultant displacement in this case will be 5 steps forward.
The resultant of a number of vectors is the single vector whose effect is the same as the individual vectors acting together.
In other words, the individual vectors can be replaced by the resultant – the overall effect is the same. If vectors and have a resultant , this can be represented mathematically as,
Let us consider some more examples of vector addition using displacements. The arrows tell you how far to move and in what direction. Arrows to the right correspond to steps forward, whilearrows to the left correspond to steps backward. Look at all of the examples below and check them.
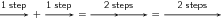
This example says 1 step forward and then another step forward is the same as an arrow twice as long – two steps forward.
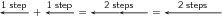
This examples says 1 step backward and then another step backward is the same as an arrow twice as long – two steps backward.
It is sometimes possible that you end up back where you started. In this case the net result of what you have done is that you have gone nowhere (your start and end points are at the same place). In this case, your resultant displacement is a vector with length zero units. We use the symbol to denote such a vector:
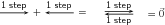
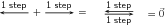
Check the following examples in the same way. Arrows up the page can be seen as steps left and arrows down the page as steps right.
Try a couple to convince yourself!
|
|
|
|
|
|
It is important to realise that the directions are not special– `forward and backwards' or `left and right' are treated in the same way. The same istrue of any set of parallel directions:
|
|
|
|
|
|
In the above examples the separate displacements were parallel to one another. However the same head-to-tail technique of vector additioncan be applied to vectors in any direction.
|
|
|
|
Now you have discovered one use for vectors; describing resultant displacement – how far and in what direction youhave travelled after a series of movements.
Although vector addition here has been demonstrated with displacements, all vectors behave in exactly the same way. Thus, ifgiven a number of forces acting on a body you can use the same method to determine the resultant force acting on the body. We will return tovector addition in more detail later.
What does it mean to subtract a vector? Well this is really simple; if we have 5 apples and we subtract 3 apples, we have only 2 apples left. Nowlets work in steps; if we take 5 steps forward and then subtract 3 steps forward we are left with only two steps forward:

What have we done? You originally took 5 steps forward but then you took 3 steps back. That backward displacement would be represented by an arrowpointing to the left (backwards) with length 3. The net result of adding these two vectors is 2 steps forward:
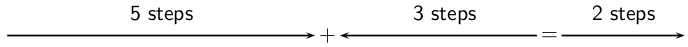
Thus, subtracting a vector from another is the same as adding a vector in the opposite direction (i.e. subtracting 3 steps forwards is the same as adding 3 steps backwards).
In the problem, motion in the forward direction has been represented by an arrow to the right. Arrows to the right are positive and arrows to the left are negative. More generally, vectors in opposite directions differ in sign (i.e. if we define up as positive, then vectors acting down are negative). Thus, changing the sign of a vectorsimply reverses its direction:
|
|
|
|
|
|
|
|
|
In mathematical form, subtracting from gives a new vector :
This clearly shows that subtracting vector from is the same as adding to . Look at the following examples of vector subtraction.

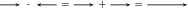
What happens when you multiply a vector by a scalar (an ordinary number)?
Going back to normal multiplication we know that is just 2 groups of 2 added together to give 4. We can adopt a similar approach to understand how vector multiplication works.
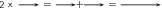

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?