| << Chapter < Page | Chapter >> Page > |
One interesting characteristic of the SHM of an object attached to a spring is that the angular frequency, and therefore the period and frequency of the motion, depend on only the mass and the force constant, and not on other factors such as the amplitude of the motion. We can use the equations of motion and Newton’s second law to find equations for the angular frequency, frequency, and period.
Consider the block on a spring on a frictionless surface. There are three forces on the mass: the weight, the normal force, and the force due to the spring. The only two forces that act perpendicular to the surface are the weight and the normal force, which have equal magnitudes and opposite directions, and thus sum to zero. The only force that acts parallel to the surface is the force due to the spring, so the net force must be equal to the force of the spring:
Substituting the equations of motion for x and a gives us
Cancelling out like terms and solving for the angular frequency yields
The angular frequency depends only on the force constant and the mass, and not the amplitude. The angular frequency is defined as which yields an equation for the period of the motion:
The period also depends only on the mass and the force constant. The greater the mass, the longer the period. The stiffer the spring, the shorter the period. The frequency is
When a spring is hung vertically and a block is attached and set in motion, the block oscillates in SHM. In this case, there is no normal force, and the net effect of the force of gravity is to change the equilibrium position. Consider [link] . Two forces act on the block: the weight and the force of the spring. The weight is constant and the force of the spring changes as the length of the spring changes.
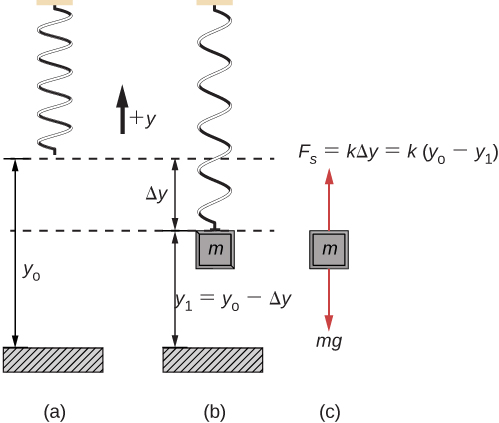
When the block reaches the equilibrium position, as seen in [link] , the force of the spring equals the weight of the block, , where
From the figure, the change in the position is and since , we have
If the block is displaced and released, it will oscillate around the new equilibrium position. As shown in [link] , if the position of the block is recorded as a function of time, the recording is a periodic function.
If the block is displaced to a position y , the net force becomes . But we found that at the equilibrium position, . Substituting for the weight in the equation yields

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?