9.5 Collisions in multiple dimensions  (Page 5/4)

It is far more common for collisions to occur in two dimensions; that is, the angle between the initial velocity vectors is neither zero nor $180\text{°}$ . Let’s see what complications arise from this.

The first idea we need is that momentum is a vector; like all vectors, it can be expressed as a sum of perpendicular components (usually, though not always, an x -component and a y -component, and a z -component if necessary). Thus, when we write down the statement of conservation of momentum for a problem, our momentum vectors can be, and usually will be, expressed in component form.

The second idea we need comes from the fact that momentum is related to force:

Expressing both the force and the momentum in component form,

Remember, these equations are simply Newton’s second law, in vector form and in component form. We know that Newton’s second law is true in each direction, independently of the others. It follows therefore (via Newton’s third law) that conservation of momentum is also true in each direction independently.

These two ideas motivate the solution to two-dimensional problems: We write down the expression for conservation of momentum twice: once in the x -direction and once in the y -direction.

This procedure is shown graphically in [link] .

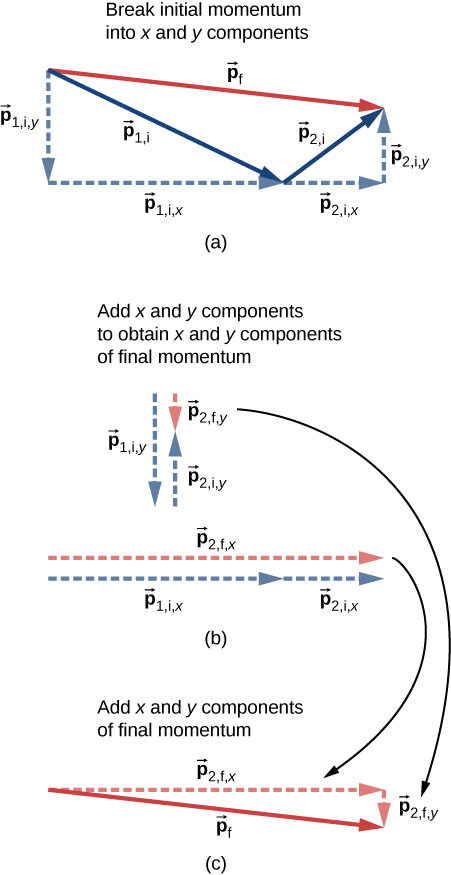
We solve each of these two component equations independently to obtain the x - and y -components of the desired velocity vector:

(Here, m represents the total mass of the system.) Finally, combine these components using the Pythagorean theorem,