9.2 Impulse and collisions (Page 12/10)

University physics volume 1 Page 1 / 10

By the end of this section, you will be able to:

Explain what an impulse is, physically
Describe what an impulse does
Relate impulses to collisions
Apply the impulse-momentum theorem to solve problems

We have defined momentum to be the product of mass and velocity. Therefore, if an object’s velocity should change (due to the application of a force on the object), then necessarily, its momentum changes as well. This indicates a connection between momentum and force. The purpose of this section is to explore and describe that connection.

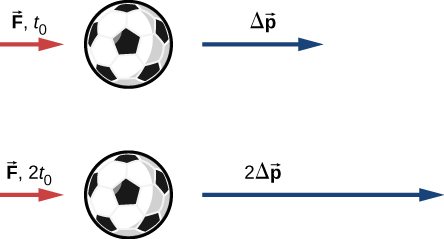
Suppose you apply a force on a free object for some amount of time. Clearly, the larger the force, the larger the object’s change of momentum will be. Alternatively, the more time you spend applying this force, again the larger the change of momentum will be, as depicted in [link] . The amount by which the object’s motion changes is therefore proportional to the magnitude of the force, and also to the time interval over which the force is applied.

Two soccer balls are shown. In one figure, a red arrow labeled vector F, t sub 0 points to the right and a blue arrow labeled delta p vector also points to the right. In the second figure, a red arrow of the same length as in the first figure points to the right and is labeled vector F, 2 t sub 0. A blue arrow twice as long as the blue arrow in the first figure points to the right and is labeled 2 delta p vector. — The change in momentum of an object is proportional to the length of time during which the force is applied. If a force is exerted on the lower ball for twice as long as on the upper ball, then the change in the momentum of the lower ball is twice that of the upper ball.

Mathematically, if a quantity is proportional to two (or more) things, then it is proportional to the product of those things. The product of a force and a time interval (over which that force acts) is called impulse , and is given the symbol $\vec{J} .$

Impulse

Let $\vec{F} (t)$ be the force applied to an object over some differential time interval dt ( [link] ). The resulting impulse on the object is defined as

d \vec{J} \equiv \vec{F} (t) d t .

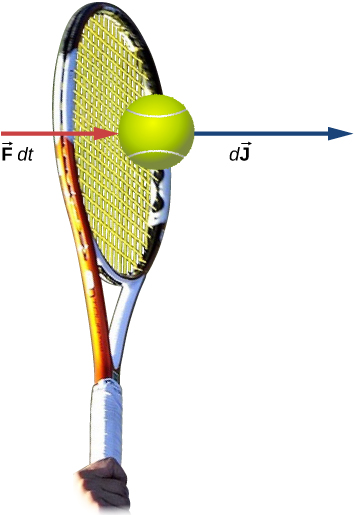
A drawing of a tennis racket hitting a tennis ball. Two arrows pointing to the right are drawn near the ball. One is labeled vector F d t and th other is labeled d J vector. — A force applied by a tennis racquet to a tennis ball over a time interval generates an impulse acting on the ball.

The total impulse over the interval $t_{f} - t_{i}$ is

\vec{J} = \int_{t_{i}}^{t_{f}} d \vec{J} or \vec{J} \equiv \int_{t_{i}}^{t_{f}} \vec{F} (t) d t .

[link] and [link] together say that when a force is applied for an infinitesimal time interval dt , it causes an infinitesimal impulse $d \vec{J}$ , and the total impulse given to the object is defined to be the sum (integral) of all these infinitesimal impulses.

To calculate the impulse using [link] , we need to know the force function F ( t ), which we often don’t. However, a result from calculus is useful here: Recall that the average value of a function over some interval is calculated by

f {(x)}_{ave} = \frac{1}{Δ x} \int_{x_{i}}^{x_{f}} f (x) d x

where $Δ x = x_{f} - x_{i}$ . Applying this to the time-dependent force function, we obtain

{\vec{F}}_{ave} = \frac{1}{Δ t} \int_{t_{i}}^{t_{f}} \vec{F} (t) d t .

Therefore, from [link] ,

\vec{J} = {\vec{F}}_{ave} Δ t .

The idea here is that you can calculate the impulse on the object even if you don’t know the details of the force as a function of time; you only need the average force. In fact, though, the process is usually reversed: You determine the impulse (by measurement or calculation) and then calculate the average force that caused that impulse.

To calculate the impulse, a useful result follows from writing the force in [link] as $\vec{F} (t) = m \vec{a} (t)$ :

\vec{J} = \int_{t_{i}}^{t_{f}} \vec{F} (t) d t = m \int_{t_{i}}^{t_{f}} \vec{a} (t) d t = m [\vec{v} (t_{f}) - {\vec{v}}_{i}] .

For a constant force ${\vec{F}}_{ave} = \vec{F} = m \vec{a}$ , this simplifies to

\vec{J} = m \vec{a} Δ t = m {\vec{v}}_{f} - m {\vec{v}}_{i} = m ({\vec{v}}_{f} - {\vec{v}}_{i}) .

That is,

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 1' conversation and receive update notifications?

Ask

	3 AP Key Terms 03 Cellular Level of Organization By OpenStax Start Key Terms
	3 Microeconomics 03 Demand Supply By OpenStax Start Flashcards
	Principles of macroeconomics for ap® courses By OpenStax Read Online Course
	8 AP 08 Appendicular Skeleton MCQ By OpenStax Start Quiz
	Does your crush like you? By Hoy Wen Start Quiz
	Corporate Communication BUS210 By P. Wynn Norman Start Quiz
	13 AP 13 Nervous System MCQ By OpenStax Start Quiz
	21 AP Key Terms 21 Lymphatic Immune System By OpenStax Start Key Terms
©flickr: Francisco	U.S. Civil War Pre-test By Danielle Stephens Start Quiz
	2 Business Law MCQ 2 By Maureen Miller Start Exam