8.4 Potential energy diagrams and stability  (Page 15/7)

Often, you can get a good deal of useful information about the dynamical behavior of a mechanical system just by interpreting a graph of its potential energy as a function of position, called a potential energy diagram    . This is most easily accomplished for a one-dimensional system, whose potential energy can be plotted in one two-dimensional graph—for example, U ( x ) versus x —on a piece of paper or a computer program. For systems whose motion is in more than one dimension, the motion needs to be studied in three-dimensional space. We will simplify our procedure for one-dimensional motion only.

First, let’s look at an object, freely falling vertically, near the surface of Earth, in the absence of air resistance. The mechanical energy of the object is conserved, $E=K+U,$ and the potential energy, with respect to zero at ground level, is $U\left(y\right)=mgy,$ which is a straight line through the origin with slope $mg$ . In the graph shown in [link] , the x -axis is the height above the ground y and the y -axis is the object’s energy.

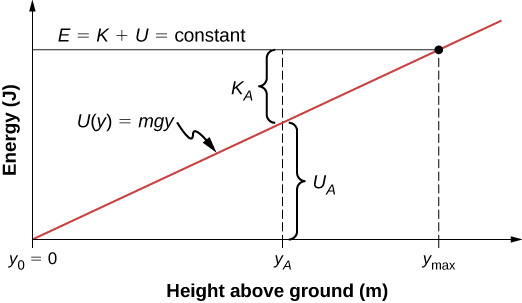
The line at energy E represents the constant mechanical energy of the object, whereas the kinetic and potential energies, $K_A$ and $U_A,$ are indicated at a particular height $y_A.$ You can see how the total energy is divided between kinetic and potential energy as the object’s height changes. Since kinetic energy can never be negative, there is a maximum potential energy and a maximum height, which an object with the given total energy cannot exceed:

If we use the gravitational potential energy reference point of zero at $y_0,$ we can rewrite the gravitational potential energy U as mgy . Solving for y results in

We note in this expression that the quantity of the total energy divided by the weight ( mg ) is located at the maximum height of the particle, or $y_{\text{max}}.$ At the maximum height, the kinetic energy and the speed are zero, so if the object were initially traveling upward, its velocity would go through zero there, and $y_{\text{max}}$ would be a turning point in the motion. At ground level, $y_0=0$ , the potential energy is zero, and the kinetic energy and the speed are maximum:

The maximum speed $\text{±}{v}_0$ gives the initial velocity necessary to reach $y_{\text{max}},$ the maximum height, and $\text{−}{v}_0$ represents the final velocity, after falling from $y_{\text{max}}.$ You can read all this information, and more, from the potential energy diagram we have shown.

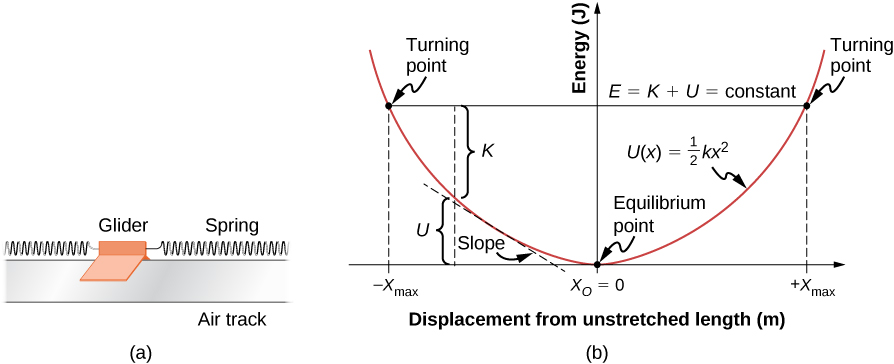
Consider a mass-spring system on a frictionless, stationary, horizontal surface, so that gravity and the normal contact force do no work and can be ignored ( [link] ). This is like a one-dimensional system, whose mechanical energy E is a constant and whose potential energy, with respect to zero energy at zero displacement from the spring’s unstretched length, $x=0,\text{is}U\left(x\right)=\frac{1}{2}k{x}^2$ .