6.3 Centripetal force  (Page 20/15)

In Motion in Two and Three Dimensions , we examined the basic concepts of circular motion. An object undergoing circular motion, like one of the race cars shown at the beginning of this chapter, must be accelerating because it is changing the direction of its velocity. We proved that this centrally directed acceleration, called centripetal acceleration    , is given by the formula

where v is the velocity of the object, directed along a tangent line to the curve at any instant. If we know the angular velocity $\omega$ , then we can use

Angular velocity gives the rate at which the object is turning through the curve, in units of rad/s. This acceleration acts along the radius of the curved path and is thus also referred to as a radial acceleration.

An acceleration must be produced by a force. Any force or combination of forces can cause a centripetal or radial acceleration. Just a few examples are the tension in the rope on a tether ball, the force of Earth’s gravity on the Moon, friction between roller skates and a rink floor, a banked roadway’s force on a car, and forces on the tube of a spinning centrifuge. Any net force causing uniform circular motion is called a centripetal force    . The direction of a centripetal force is toward the center of curvature, the same as the direction of centripetal acceleration. According to Newton’s second law of motion, net force is mass times acceleration: $F_{\text{net}}=ma.$ For uniform circular motion, the acceleration is the centripetal acceleration: _. $a=a_{\text{c}}.$ Thus, the magnitude of centripetal force $F_{\text{c}}$ is

By substituting the expressions for centripetal acceleration $a_{\text{c}}$ $(a_{\text{c}}=\frac{v^2}{r};a_{\text{c}}=r{\omega }^2),$ we get two expressions for the centripetal force $F_{\text{c}}$ in terms of mass, velocity, angular velocity, and radius of curvature:

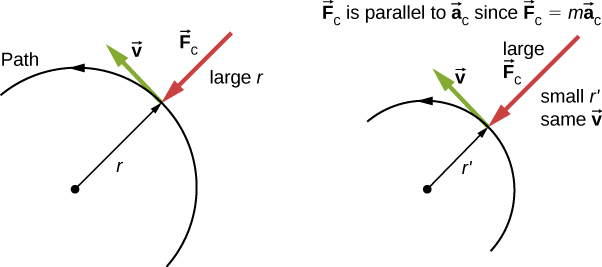
You may use whichever expression for centripetal force is more convenient. Centripetal force ${\overrightarrow{F}}_{\text{c}}$ is always perpendicular to the path and points to the center of curvature, because ${\overrightarrow{a}}_{\text{c}}$ is perpendicular to the velocity and points to the center of curvature. Note that if you solve the first expression for r , you get

This implies that for a given mass and velocity, a large centripetal force causes a small radius of curvature—that is, a tight curve, as in [link] .

What coefficient of friction do cars need on a flat curve?