4.1 Displacement and velocity vectors  (Page 23/7)

Displacement and velocity in two or three dimensions are straightforward extensions of the one-dimensional definitions. However, now they are vector quantities, so calculations with them have to follow the rules of vector algebra, not scalar algebra.

Displacement vector

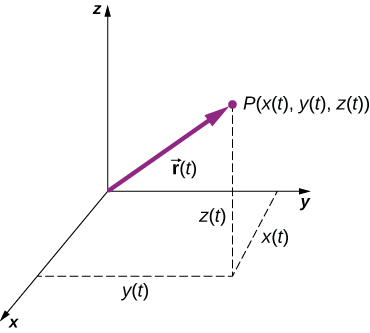
To describe motion in two and three dimensions, we must first establish a coordinate system and a convention for the axes. We generally use the coordinates x , y , and z to locate a particle at point P ( x , y , z ) in three dimensions. If the particle is moving, the variables x , y , and z are functions of time ( t ):

The position vector    from the origin of the coordinate system to point P is $\overrightarrow{r}(t).$ In unit vector notation, introduced in Coordinate Systems and Components of a Vector , $\overrightarrow{r}(t)$ is

[link] shows the coordinate system and the vector to point P , where a particle could be located at a particular time t . Note the orientation of the x , y , and z axes. This orientation is called a right-handed coordinate system ( Coordinate Systems and Components of a Vector ) and it is used throughout the chapter.

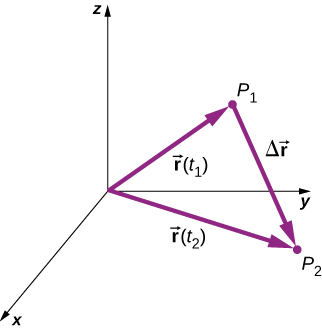
With our definition of the position of a particle in three-dimensional space, we can formulate the three-dimensional displacement. [link] shows a particle at time $t_1$ located at $P_1$ with position vector $\overrightarrow{r}(t_1).$ At a later time $t_2,$ the particle is located at $P_2$ with position vector $\overrightarrow{r}(t_2)$ . The displacement vector     $\text{Δ}\overrightarrow{r}$ is found by subtracting $\overrightarrow{r}(t_1)$ from $\overrightarrow{r}(t_2):$

Vector addition is discussed in Vectors . Note that this is the same operation we did in one dimension, but now the vectors are in three-dimensional space.

The following examples illustrate the concept of displacement in multiple dimensions.

Polar orbiting satellite

A satellite is in a circular polar orbit around Earth at an altitude of 400 km—meaning, it passes directly overhead at the North and South Poles. What is the magnitude and direction of the displacement vector from when it is directly over the North Pole to when it is at $\mathrm{-45}\text{°}$ latitude?

Strategy

We make a picture of the problem to visualize the solution graphically. This will aid in our understanding of the displacement. We then use unit vectors to solve for the displacement.

Solution

[link] shows the surface of Earth and a circle that represents the orbit of the satellite. Although satellites are moving in three-dimensional space, they follow trajectories of ellipses, which can be graphed in two dimensions. The position vectors are drawn from the center of Earth, which we take to be the origin of the coordinate system, with the y -axis as north and the x -axis as east. The vector between them is the displacement of the satellite. We take the radius of Earth as 6370 km, so the length of each position vector is 6770 km.

Got questions? Get instant answers now!