3.5 Free fall  (Page 25/7)

An interesting application of [link] through [link] is called free fall , which describes the motion of an object falling in a gravitational field, such as near the surface of Earth or other celestial objects of planetary size. Let’s assume the body is falling in a straight line perpendicular to the surface, so its motion is one-dimensional. For example, we can estimate the depth of a vertical mine shaft by dropping a rock into it and listening for the rock to hit the bottom. But “falling,” in the context of free fall, does not necessarily imply the body is moving from a greater height to a lesser height. If a ball is thrown upward, the equations of free fall apply equally to its ascent as well as its descent.

Gravity

The most remarkable and unexpected fact about falling objects is that if air resistance and friction are negligible, then in a given location all objects fall toward the center of Earth with the same constant acceleration , independent of their mass . This experimentally determined fact is unexpected because we are so accustomed to the effects of air resistance and friction that we expect light objects to fall slower than heavy ones. Until Galileo Galilei (1564–1642) proved otherwise, people believed that a heavier object has a greater acceleration in a free fall. We now know this is not the case. In the absence of air resistance, heavy objects arrive at the ground at the same time as lighter objects when dropped from the same height [link] .

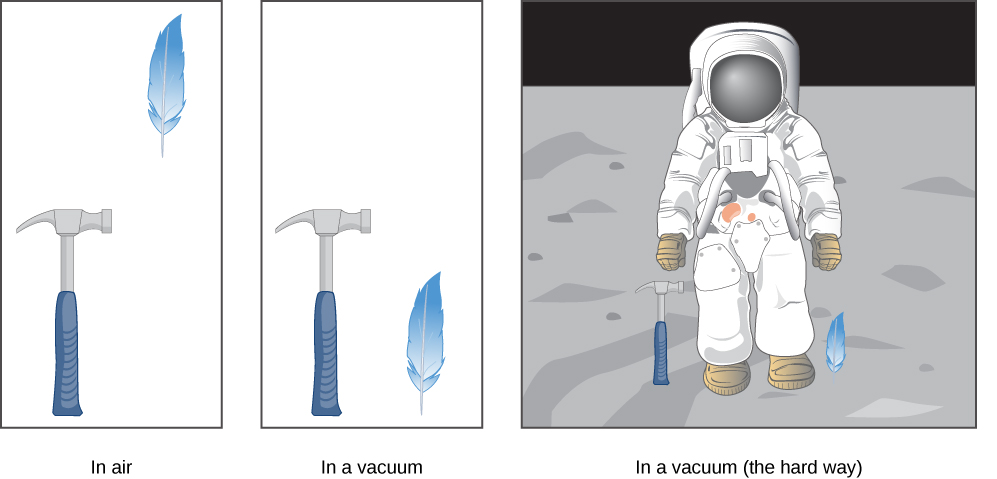
In the real world, air resistance can cause a lighter object to fall slower than a heavier object of the same size. A tennis ball reaches the ground after a baseball dropped at the same time. (It might be difficult to observe the difference if the height is not large.) Air resistance opposes the motion of an object through the air, and friction between objects—such as between clothes and a laundry chute or between a stone and a pool into which it is dropped—also opposes motion between them.

For the ideal situations of these first few chapters, an object falling without air resistance or friction is defined to be in free fall    . The force of gravity causes objects to fall toward the center of Earth. The acceleration of free-falling objects is therefore called acceleration due to gravity    . Acceleration due to gravity is constant, which means we can apply the kinematic equations to any falling object where air resistance and friction are negligible. This opens to us a broad class of interesting situations.