| << Chapter < Page | Chapter >> Page > |
When you’re in motion, the basic questions to ask are: Where are you? Where are you going? How fast are you getting there? The answers to these questions require that you specify your position, your displacement, and your average velocity—the terms we define in this section.
To describe the motion of an object, you must first be able to describe its position ( x ): where it is at any particular time . More precisely, we need to specify its position relative to a convenient frame of reference. A frame of reference is an arbitrary set of axes from which the position and motion of an object are described. Earth is often used as a frame of reference, and we often describe the position of an object as it relates to stationary objects on Earth. For example, a rocket launch could be described in terms of the position of the rocket with respect to Earth as a whole, whereas a cyclist’s position could be described in terms of where she is in relation to the buildings she passes [link] . In other cases, we use reference frames that are not stationary but are in motion relative to Earth. To describe the position of a person in an airplane, for example, we use the airplane, not Earth, as the reference frame. To describe the position of an object undergoing one-dimensional motion, we often use the variable x . Later in the chapter, during the discussion of free fall, we use the variable y .

If an object moves relative to a frame of reference—for example, if a professor moves to the right relative to a whiteboard [link] —then the object’s position changes. This change in position is called displacement . The word displacement implies that an object has moved, or has been displaced. Although position is the numerical value of x along a straight line where an object might be located, displacement gives the change in position along this line. Since displacement indicates direction, it is a vector and can be either positive or negative, depending on the choice of positive direction. Also, an analysis of motion can have many displacements embedded in it. If right is positive and an object moves 2 m to the right, then 4 m to the left, the individual displacements are 2 m and m, respectively.
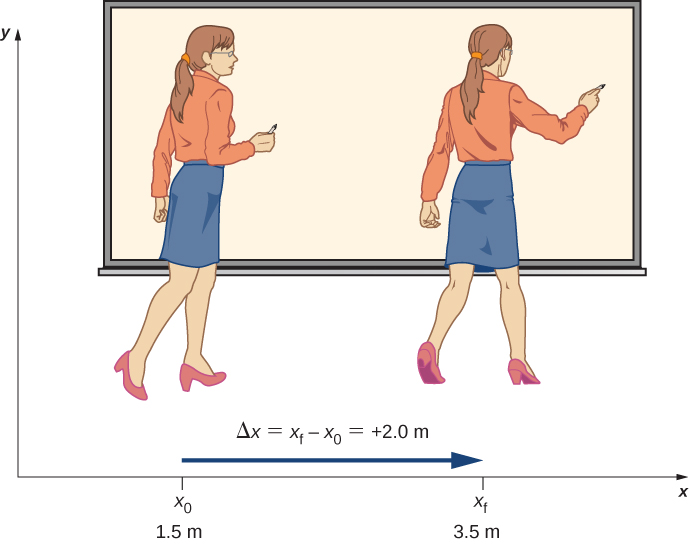
Displacement is the change in position of an object:
where is displacement, is the final position, and is the initial position.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?