2.2 Coordinate systems and components of a vector  (Page 31/15)

Vectors are usually described in terms of their components in a coordinate system . Even in everyday life we naturally invoke the concept of orthogonal projections in a rectangular coordinate system. For example, if you ask someone for directions to a particular location, you will more likely be told to go 40 km east and 30 km north than 50 km in the direction $37\text{°}$ north of east.

In a rectangular (Cartesian) xy -coordinate system in a plane, a point in a plane is described by a pair of coordinates ( x , y ). In a similar fashion, a vector $\overrightarrow{A}$ in a plane is described by a pair of its vector coordinates. The x -coordinate of vector $\overrightarrow{A}$ is called its x -component and the y -coordinate of vector $\overrightarrow{A}$ is called its y -component. The vector x -component is a vector denoted by ${\overrightarrow{A}}_x$ . The vector y -component is a vector denoted by ${\overrightarrow{A}}_y$ . In the Cartesian system, the x and y vector components    of a vector are the orthogonal projections of this vector onto the x - and y -axes, respectively. In this way, following the parallelogram rule for vector addition, each vector on a Cartesian plane can be expressed as the vector sum of its vector components:

As illustrated in [link] , vector $\overrightarrow{A}$ is the diagonal of the rectangle where the x -component ${\overrightarrow{A}}_x$ is the side parallel to the x -axis and the y -component ${\overrightarrow{A}}_y$ is the side parallel to the y -axis. Vector component ${\overrightarrow{A}}_x$ is orthogonal to vector component ${\overrightarrow{A}}_y$ .

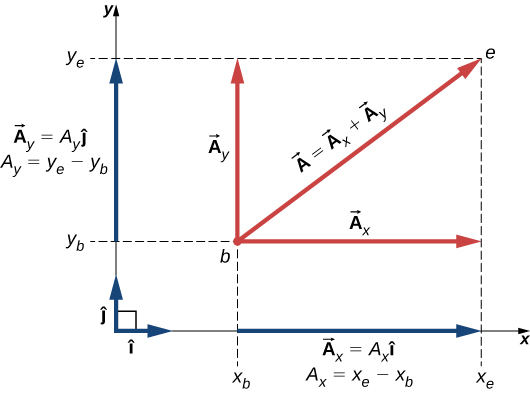
It is customary to denote the positive direction on the x -axis by the unit vector $\widehat{i}$ and the positive direction on the y -axis by the unit vector $\widehat{j}$ . Unit vectors of the axes , $\widehat{i}$ and $\widehat{j}$ , define two orthogonal directions in the plane. As shown in [link] , the x - and y - components of a vector can now be written in terms of the unit vectors of the axes:

The vectors ${\overrightarrow{A}}_x$ and ${\overrightarrow{A}}_y$ defined by [link] are the vector components of vector $\overrightarrow{A}$ . The numbers $A_x$ and $A_y$ that define the vector components in [link] are the scalar component     s of vector $\overrightarrow{A}$ . Combining [link] with [link] , we obtain the component form of a vector :

If we know the coordinates $b(x_b,y_b)$ of the origin point of a vector (where b stands for “beginning”) and the coordinates $e(x_e,y_e)$ of the end point of a vector (where e stands for “end”), we can obtain the scalar components of a vector simply by subtracting the origin point coordinates from the end point coordinates: