1. Home
  2. University physics volume 1
  3. Unit 2. waves and acoustics
  4. Sound
  5. Sound intensity

17.3 Sound intensity

<< Chapter < Page
  University physics volume 1     Page 1 / 14
Chapter >> Page >
By the end of this section, you will be able to:
  • Define the term intensity
  • Explain the concept of sound intensity level
  • Describe how the human ear translates sound

In a quiet forest, you can sometimes hear a single leaf fall to the ground. But when a passing motorist has his stereo turned up, you cannot even hear what the person next to you in your car is saying ( [link] ). We are all very familiar with the loudness of sounds and are aware that loudness is related to how energetically the source is vibrating. High noise exposure is hazardous to hearing, which is why it is important for people working in industrial settings to wear ear protection. The relevant physical quantity is sound intensity, a concept that is valid for all sounds whether or not they are in the audible range.

Photograph shows a roadway crowded with cars and motorcycles in Delhi.
Noise on crowded roadways, like this one in Delhi, makes it hard to hear others unless they shout. (credit: “Lingaraj G J”/Flickr)

In Waves , we defined intensity as the power per unit area carried by a wave. Power is the rate at which energy is transferred by the wave. In equation form, intensity I is

I = P A ,

where P is the power through an area A . The SI unit for I is W/m 2 . If we assume that the sound wave is spherical, and that no energy is lost to thermal processes, the energy of the sound wave is spread over a larger area as distance increases, so the intensity decreases. The area of a sphere is A = 4 π r 2 . As the wave spreads out from r 1 to r 2 , the energy also spreads out over a larger area:

P 1 = P 2 I 1 4 π r 1 2 = I 2 4 π r 2 2 ;
I 2 = I 1 ( r 1 r 2 ) 2 .

The intensity decreases as the wave moves out from the source. In an inverse square relationship, such as the intensity, when you double the distance, the intensity decreases to one quarter,

I 2 = I 1 ( r 1 r 2 ) 2 = I 1 ( r 1 2 r 1 ) 2 = 1 4 I 1 .

Generally, when considering the intensity of a sound wave, we take the intensity to be the time-averaged value of the power, denoted by ⟨ P ⟩ , divided by the area,

I = ⟨ P ⟩ A .

The intensity of a sound wave is proportional to the change in the pressure squared and inversely proportional to the density and the speed. Consider a parcel of a medium initially undisturbed and then influenced by a sound wave at time t , as shown in [link] .

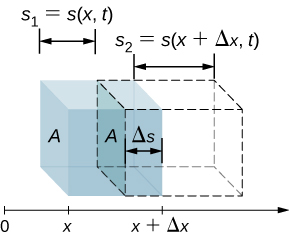
Picture is a drawing of a parcel of a medium initially undisturbed and then influenced by a sound wave. A sound wave moves through the medium at time t, and the parcel is displaced and expands in the displacement direction.
An undisturbed parcel of a medium with a volume V = A Δ x shown in blue. A sound wave moves through the medium at time t , and the parcel is displaced and expands, as shown by dotted lines. The change in volume is Δ V = A Δ s = A ( s 2 − s 1 ) , where s 1 is the displacement of the leading edge of the parcel and s 2 is the displacement of the trailing edge of the parcel. In the figure, s 2 > s 1 and the parcel expands, but the parcel can either expand or compress ( s 2 < s 1 ) , depending on which part of the sound wave (compression or rarefaction) is moving through the parcel.

As the sound wave moves through the parcel, the parcel is displaced and may expand or contract. If s 2 > s 1 , the volume has increased and the pressure decreases. If s 2 < s 1 , the volume has decreased and the pressure increases. The change in the volume is

Δ V = A Δ s = A ( s 2 − s 1 ) = A ( s ( x + Δ x , t ) − s ( x , t ) ) .

The fractional change in the volume is the change in volume divided by the original volume:
<< Chapter < Page Page > Chapter >>
Practice Key Terms 8

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 1' conversation and receive update notifications?

Ask