17.2 Speed of sound  (Page 23/6)

Sound, like all waves, travels at a certain speed and has the properties of frequency and wavelength. You can observe direct evidence of the speed of sound while watching a fireworks display ( [link] ). You see the flash of an explosion well before you hear its sound and possibly feel the pressure wave, implying both that sound travels at a finite speed and that it is much slower than light.

The difference between the speed of light and the speed of sound can also be experienced during an electrical storm. The flash of lighting is often seen before the clap of thunder. You may have heard that if you count the number of seconds between the flash and the sound, you can estimate the distance to the source. Every five seconds converts to about one mile. The velocity of any wave is related to its frequency and wavelength by

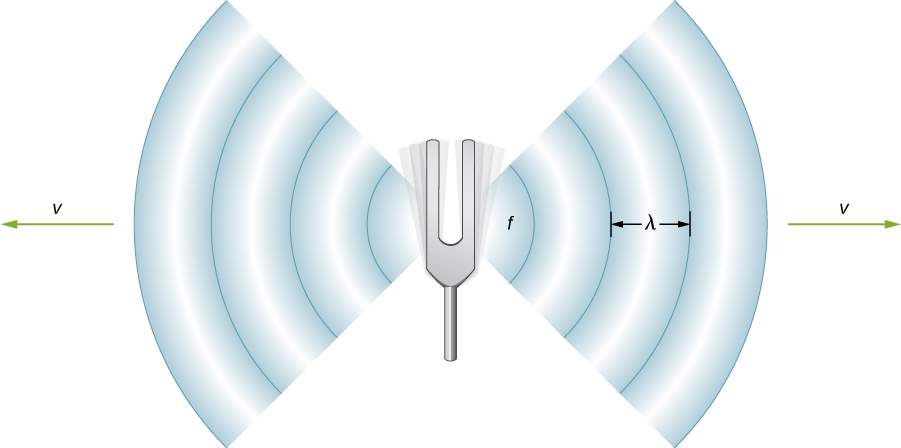
where v is the speed of the wave, f is its frequency, and $\lambda$ is its wavelength. Recall from Waves that the wavelength    is the length of the wave as measured between sequential identical points. For example, for a surface water wave or sinusoidal wave on a string, the wavelength can be measured between any two convenient sequential points with the same height and slope, such as between two sequential crests or two sequential troughs. Similarly, the wavelength of a sound wave is the distance between sequential identical parts of a wave—for example, between sequential compressions ( [link] ). The frequency is the same as that of the source and is the number of waves that pass a point per unit time.

Speed of sound in various media

[link] shows that the speed of sound varies greatly in different media. The speed of sound in a medium depends on how quickly vibrational energy can be transferred through the medium. For this reason, the derivation of the speed of sound in a medium depends on the medium and on the state of the medium. In general, the equation for the speed of a mechanical wave in a medium depends on the square root of the restoring force, or the elastic property , divided by the inertial property ,

Also, sound waves satisfy the wave equation derived in Waves ,

Recall from Waves that the speed of a wave on a string is equal to $v=\sqrt{\frac{F_T}{\mu }},$ where the restoring force is the tension in the string $F_T$ and the linear density $\mu$ is the inertial property. In a fluid, the speed of sound depends on the bulk modulus and the density,

The speed of sound in a solid the depends on the Young’s modulus    of the medium and the density,