16.2 Mathematics of waves  (Page 14/11)

In the previous section, we described periodic waves by their characteristics of wavelength, period, amplitude, and wave speed of the wave. Waves can also be described by the motion of the particles of the medium through which the waves move. The position of particles of the medium can be mathematically modeled as wave function     s , which can be used to find the position, velocity, and acceleration of the particles of the medium of the wave at any time.

Pulses

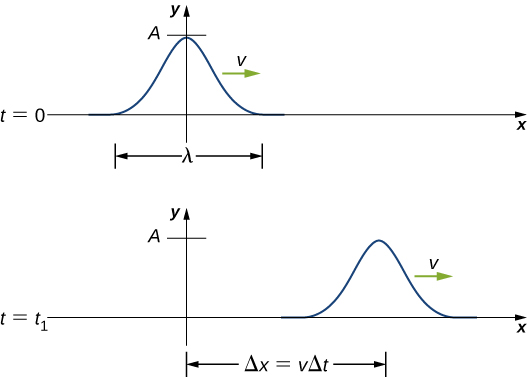
A pulse    can be described as wave consisting of a single disturbance that moves through the medium with a constant amplitude. The pulse moves as a pattern that maintains its shape as it propagates with a constant wave speed. Because the wave speed is constant, the distance the pulse moves in a time $\text{Δ}t$ is equal to $\text{Δ}x=v\text{Δ}t$ ( [link] ).

Modeling a one-dimensional sinusoidal wave using a wave function

Consider a string kept at a constant tension $F_T$ where one end is fixed and the free end is oscillated between $y=\text{+}A$ and $y=\text{−}A$ by a mechanical device at a constant frequency. [link] shows snapshots of the wave at an interval of an eighth of a period, beginning after one period $\left(t=T\right).$

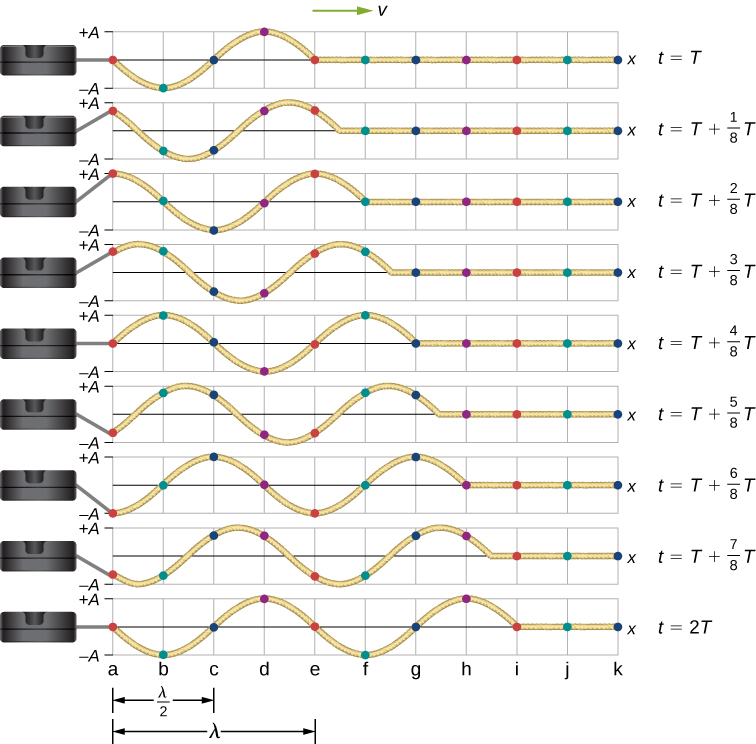
Notice that each select point on the string (marked by colored dots) oscillates up and down in simple harmonic motion, between $y=+A$ and $y=\text{−}A,$ with a period T . The wave on the string is sinusoidal and is translating in the positive x -direction as time progresses.

At this point, it is useful to recall from your study of algebra that if f ( x ) is some function, then $f\left(x-d\right)$ is the same function translated in the positive x -direction by a distance d . The function $f\left(x+d\right)$ is the same function translated in the negative x -direction by a distance d . We want to define a wave function that will give the y -position of each segment of the string for every position x along the string for every time t .

Looking at the first snapshot in [link] , the y -position of the string between $x=0$ and $x=\lambda$ can be modeled as a sine function. This wave propagates down the string one wavelength in one period, as seen in the last snapshot. The wave therefore moves with a constant wave speed of $v=\lambda \text{/}T.$

Recall that a sine function is a function of the angle $\theta$ , oscillating between $\text{+}1$ and $\mathrm{-1}$ , and repeating every $2\pi$ radians ( [link] ). However, the y -position of the medium, or the wave function, oscillates between $\text{+}A$ and $\text{−}A$ , and repeats every wavelength $\lambda$ .