14.6 Bernoulli’s equation  (Page 31/8)

As we showed in [link] , when a fluid flows into a narrower channel, its speed increases. That means its kinetic energy also increases. The increased kinetic energy comes from the net work done on the fluid to push it into the channel. Also, if the fluid changes vertical position, work is done on the fluid by the gravitational force.

A pressure difference occurs when the channel narrows. This pressure difference results in a net force on the fluid because the pressure times the area equals the force, and this net force does work. Recall the work-energy theorem,

The net work done increases the fluid’s kinetic energy. As a result, the pressure drops in a rapidly moving fluid whether or not the fluid is confined to a tube.

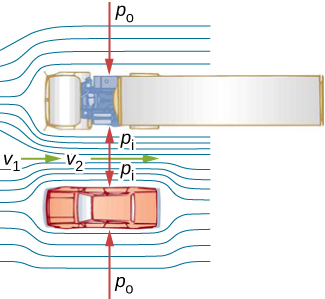
There are many common examples of pressure dropping in rapidly moving fluids. For instance, shower curtains have a disagreeable habit of bulging into the shower stall when the shower is on. The reason is that the high-velocity stream of water and air creates a region of lower pressure inside the shower, whereas the pressure on the other side remains at the standard atmospheric pressure. This pressure difference results in a net force, pushing the curtain inward. Similarly, when a car passes a truck on the highway, the two vehicles seem to pull toward each other. The reason is the same: The high velocity of the air between the car and the truck creates a region of lower pressure between the vehicles, and they are pushed together by greater pressure on the outside ( [link] ). This effect was observed as far back as the mid-1800s, when it was found that trains passing in opposite directions tipped precariously toward one another.

Energy conservation and bernoulli’s equation

The application of the principle of conservation of energy to frictionless laminar flow leads to a very useful relation between pressure and flow speed in a fluid. This relation is called Bernoulli’s equation    , named after Daniel Bernoulli (1700–1782), who published his studies on fluid motion in his book Hydrodynamica (1738).

Consider an incompressible fluid flowing through a pipe that has a varying diameter and height, as shown in [link] . Subscripts 1 and 2 in the figure denote two locations along the pipe and illustrate the relationships between the areas of the cross sections A , the speed of flow v , the height from ground y , and the pressure p at each point. We assume here that the density at the two points is the same—therefore, density is denoted by $\rho$ without any subscripts—and since the fluid in incompressible, the shaded volumes must be equal.