| << Chapter < Page | Chapter >> Page > |
Within a reasonably sized laboratory on Earth, the gravitational field is essentially uniform. The corollary states that any physical experiments performed there have the identical results as those done in a laboratory accelerating at in deep space, well away from all other masses. [link] illustrates the concept.
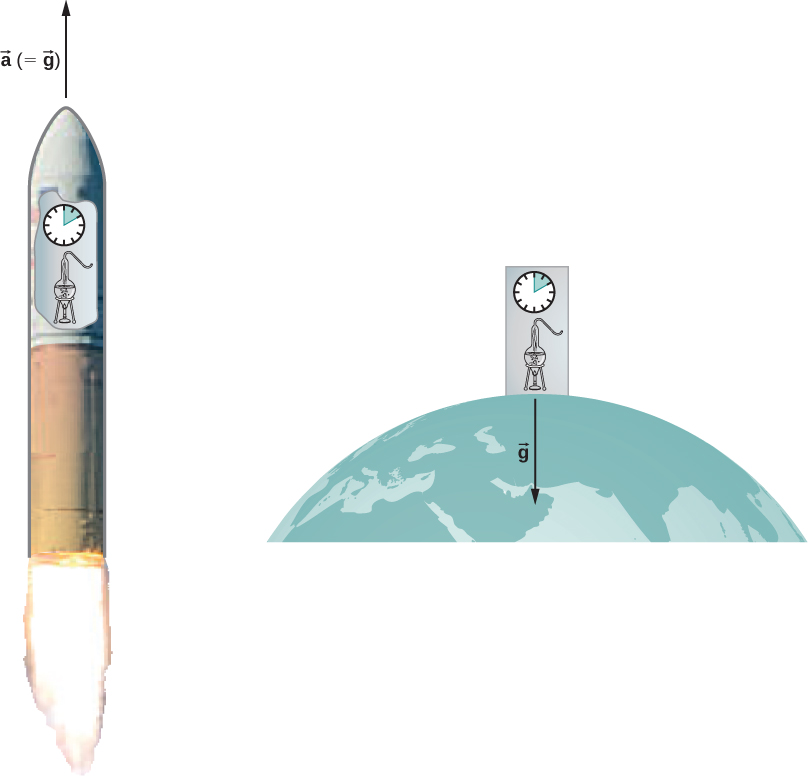
How can these two apparently fundamentally different situations be the same? The answer is that gravitation is not a force between two objects but is the result of each object responding to the effect that the other has on the space-time surrounding it. A uniform gravitational field and a uniform acceleration have exactly the same effect on space-time.
Euclidian geometry assumes a “flat” space in which, among the most commonly known attributes, a straight line is the shortest distance between two points, the sum of the angles of all triangles must be 180 degrees, and parallel lines never intersect. Non-Euclidean geometry was not seriously investigated until the nineteenth century, so it is not surprising that Euclidean space is inherently assumed in all of Newton’s laws.
The general theory of relativity challenges this long-held assumption. Only empty space is flat. The presence of mass—or energy, since relativity does not distinguish between the two—distorts or curves space and time, or space-time, around it. The motion of any other mass is simply a response to this curved space-time. [link] is a two-dimensional representation of a smaller mass orbiting in response to the distorted space created by the presence of a larger mass. In a more precise but confusing picture, we would also see space distorted by the orbiting mass, and both masses would be in motion in response to the total distortion of space. Note that the figure is a representation to help visualize the concept. These are distortions in our three-dimensional space and time. We do not see them as we would a dimple on a ball. We see the distortion only by careful measurements of the motion of objects and light as they move through space.

For weak gravitational fields, the results of general relativity do not differ significantly from Newton’s law of gravitation. But for intense gravitational fields, the results diverge, and general relativity has been shown to predict the correct results. Even in our Sun’s relatively weak gravitational field at the distance of Mercury’s orbit, we can observe the effect. Starting in the mid-1800s, Mercury’s elliptical orbit has been carefully measured. However, although it is elliptical, its motion is complicated by the fact that the perihelion position of the ellipse slowly advances. Most of the advance is due to the gravitational pull of other planets, but a small portion of that advancement could not be accounted for by Newton’s law. At one time, there was even a search for a “companion” planet that would explain the discrepancy. But general relativity correctly predicts the measurements. Since then, many measurements, such as the deflection of light of distant objects by the Sun, have verified that general relativity correctly predicts the observations.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?