| << Chapter < Page | Chapter >> Page > |
So far, we have looked at the angular momentum of systems consisting of point particles and rigid bodies. We have also analyzed the torques involved, using the expression that relates the external net torque to the change in angular momentum, [link] . Examples of systems that obey this equation include a freely spinning bicycle tire that slows over time due to torque arising from friction, or the slowing of Earth’s rotation over millions of years due to frictional forces exerted on tidal deformations.
However, suppose there is no net external torque on the system, In this case, [link] becomes the law of conservation of angular momentum .
The angular momentum of a system of particles around a point in a fixed inertial reference frame is conserved if there is no net external torque around that point:
or
Note that the total angular momentum is conserved. Any of the individual angular momenta can change as long as their sum remains constant. This law is analogous to linear momentum being conserved when the external force on a system is zero.
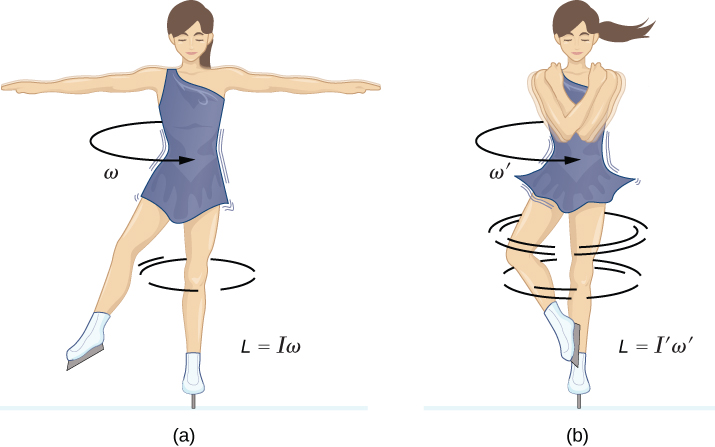
As an example of conservation of angular momentum, [link] shows an ice skater executing a spin. The net torque on her is very close to zero because there is relatively little friction between her skates and the ice. Also, the friction is exerted very close to the pivot point. Both are small, so is negligible. Consequently, she can spin for quite some time. She can also increase her rate of spin by pulling her arms and legs in. Why does pulling her arms and legs in increase her rate of spin? The answer is that her angular momentum is constant, so that
or
where the primed quantities refer to conditions after she has pulled in her arms and reduced her moment of inertia. Because is smaller, the angular velocity must increase to keep the angular momentum constant.
It is interesting to see how the rotational kinetic energy of the skater changes when she pulls her arms in. Her initial rotational energy is
whereas her final rotational energy is
Since we can substitute for and find
Because her moment of inertia has decreased, her final rotational kinetic energy has increased. The source of this additional rotational kinetic energy is the work required to pull her arms inward. Note that the skater’s arms do not move in a perfect circle—they spiral inward. This work causes an increase in the rotational kinetic energy, while her angular momentum remains constant. Since she is in a frictionless environment, no energy escapes the system. Thus, if she were to extend her arms to their original positions, she would rotate at her original angular velocity and her kinetic energy would return to its original value.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?