10.6 Torque  (Page 22/6)

An important quantity for describing the dynamics of a rotating rigid body is torque. We see the application of torque in many ways in our world. We all have an intuition about torque, as when we use a large wrench to unscrew a stubborn bolt. Torque is at work in unseen ways, as when we press on the accelerator in a car, causing the engine to put additional torque on the drive train. Or every time we move our bodies from a standing position, we apply a torque to our limbs. In this section, we define torque and make an argument for the equation for calculating torque for a rigid body with fixed-axis rotation.

Defining torque

So far we have defined many variables that are rotational equivalents to their translational counterparts. Let’s consider what the counterpart to force must be. Since forces change the translational motion of objects, the rotational counterpart must be related to changing the rotational motion of an object about an axis. We call this rotational counterpart torque    .

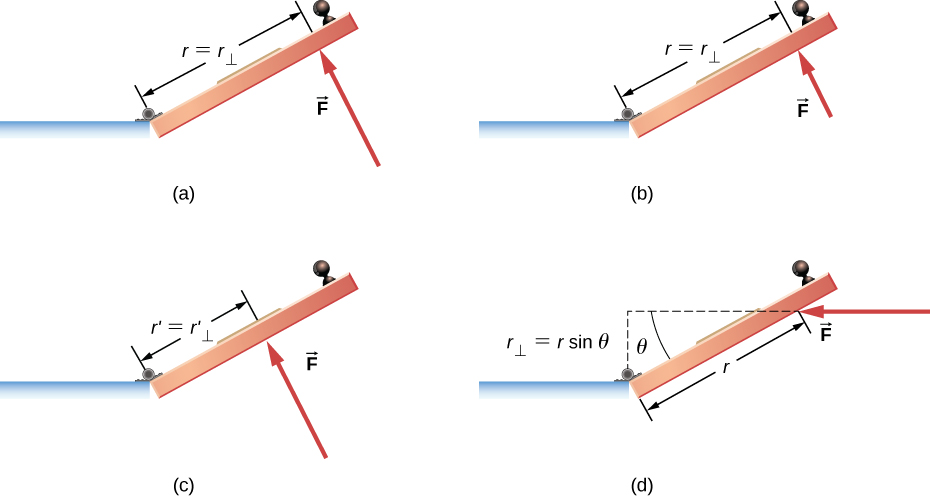
In everyday life, we rotate objects about an axis all the time, so intuitively we already know much about torque. Consider, for example, how we rotate a door to open it. First, we know that a door opens slowly if we push too close to its hinges; it is more efficient to rotate a door open if we push far from the hinges. Second, we know that we should push perpendicular to the plane of the door; if we push parallel to the plane of the door, we are not able to rotate it. Third, the larger the force, the more effective it is in opening the door; the harder you push, the more rapidly the door opens. The first point implies that the farther the force is applied from the axis of rotation, the greater the angular acceleration; the second implies that the effectiveness depends on the angle at which the force is applied; the third implies that the magnitude of the force must also be part of the equation. Note that for rotation in a plane, torque has two possible directions. Torque is either clockwise or counterclockwise relative to the chosen pivot point. [link] shows counterclockwise rotations.