24.1 Maxwell’s equations: electromagnetic waves predicted and  (Page 2/10)

Since changing electric fields create relatively weak magnetic fields, they could not be easily detected at the time of Maxwell’s hypothesis. Maxwell realized, however, that oscillating charges, like those in AC circuits, produce changing electric fields. He predicted that these changing fields would propagate from the source like waves generated on a lake by a jumping fish.

The waves predicted by Maxwell would consist of oscillating electric and magnetic fields—defined to be an electromagnetic wave (EM wave). Electromagnetic waves would be capable of exerting forces on charges great distances from their source, and they might thus be detectable. Maxwell calculated that electromagnetic waves would propagate at a speed given by the equation

When the values for ${\mu }_0$ and ${\epsilon }_0$ are entered into the equation for $c$ , we find that

which is the speed of light. In fact, Maxwell concluded that light is an electromagnetic wave having such wavelengths that it can be detected by the eye.

Other wavelengths should exist—it remained to be seen if they did. If so, Maxwell’s theory and remarkable predictions would be verified, the greatest triumph of physics since Newton. Experimental verification came within a few years, but not before Maxwell’s death.

Hertz’s observations

The German physicist Heinrich Hertz (1857–1894) was the first to generate and detect certain types of electromagnetic waves in the laboratory. Starting in 1887, he performed a series of experiments that not only confirmed the existence of electromagnetic waves, but also verified that they travel at the speed of light.

Hertz used an AC $\text{RLC}$ (resistor-inductor-capacitor) circuit that resonates at a known frequency $f_0=\frac{1}{\mathrm{2\pi }\sqrt{\text{LC}}}$ and connected it to a loop of wire as shown in [link] . High voltages induced across the gap in the loop produced sparks that were visible evidence of the current in the circuit and that helped generate electromagnetic waves.

Across the laboratory, Hertz had another loop attached to another $\text{RLC}$ circuit, which could be tuned (as the dial on a radio) to the same resonant frequency as the first and could, thus, be made to receive electromagnetic waves. This loop also had a gap across which sparks were generated, giving solid evidence that electromagnetic waves had been received.

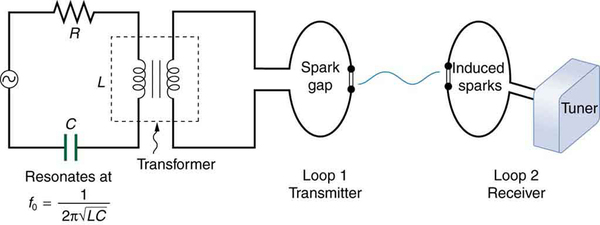
Hertz also studied the reflection, refraction, and interference patterns of the electromagnetic waves he generated, verifying their wave character. He was able to determine wavelength from the interference patterns, and knowing their frequency, he could calculate the propagation speed using the equation $\upsilon =\mathrm{f\lambda }$ (velocity—or speed—equals frequency times wavelength). Hertz was thus able to prove that electromagnetic waves travel at the speed of light. The SI unit for frequency, the hertz ( $\mathrm{1\; Hz}=\text{1 cycle/sec}$ ), is named in his honor.

Section summary

• Electromagnetic waves consist of oscillating electric and magnetic fields and propagate at the speed of light $c$ . They were predicted by Maxwell, who also showed that
  $c=\frac{1}{\sqrt{{\mu }_0{\epsilon }_0}},$

  where ${\mu }_0$ is the permeability of free space and ${\epsilon }_0$ is the permittivity of free space.

• Maxwell’s prediction of electromagnetic waves resulted from his formulation of a complete and symmetric theory of electricity and magnetism, known as Maxwell’s equations.
• These four equations are paraphrased in this text, rather than presented numerically, and encompass the major laws of electricity and magnetism. First is Gauss’s law for electricity, second is Gauss’s law for magnetism, third is Faraday’s law of induction, including Lenz’s law, and fourth is Ampere’s law in a symmetric formulation that adds another source of magnetism—changing electric fields.

Problems&Exercises