| << Chapter < Page | Chapter >> Page > |
We solve this for , noting that mass cancels, and obtain
Solution for (b)
Substituting the knowns,
(Because coefficients of friction are approximate, the answer is given to only two digits.)
Discussion
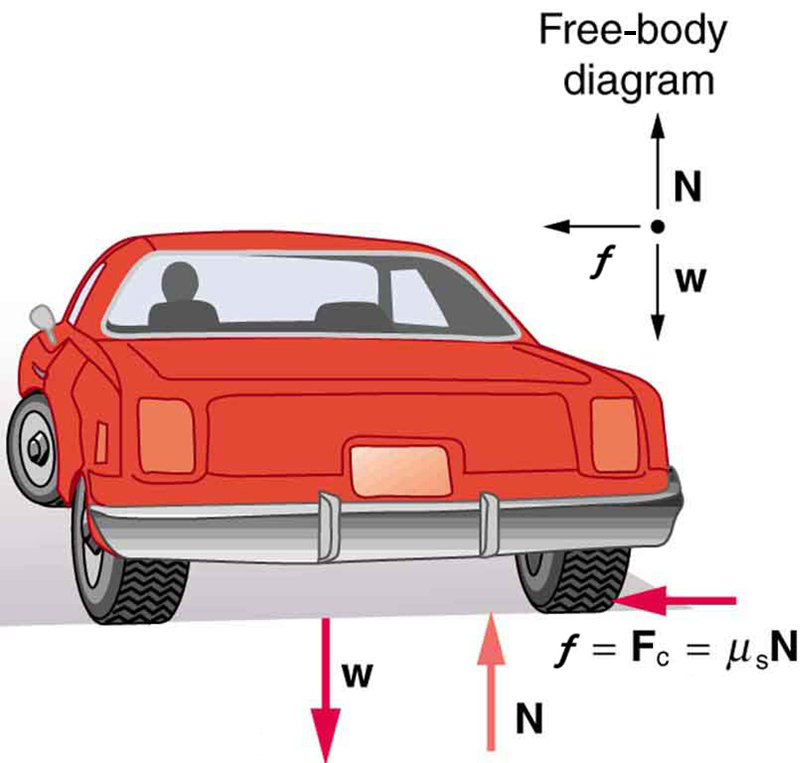
We could also solve part (a) using the first expression in because and are given. The coefficient of friction found in part (b) is much smaller than is typically found between tires and roads. The car will still negotiate the curve if the coefficient is greater than 0.13, because static friction is a responsive force, being able to assume a value less than but no more than . A higher coefficient would also allow the car to negotiate the curve at a higher speed, but if the coefficient of friction is less, the safe speed would be less than 25 m/s. Note that mass cancels, implying that in this example, it does not matter how heavily loaded the car is to negotiate the turn. Mass cancels because friction is assumed proportional to the normal force, which in turn is proportional to mass. If the surface of the road were banked, the normal force would be less as will be discussed below.
Let us now consider banked curves , where the slope of the road helps you negotiate the curve. See [link] . The greater the angle , the faster you can take the curve. Race tracks for bikes as well as cars, for example, often have steeply banked curves. In an “ideally banked curve,” the angle is such that you can negotiate the curve at a certain speed without the aid of friction between the tires and the road. We will derive an expression for for an ideally banked curve and consider an example related to it.
For ideal banking , the net external force equals the horizontal centripetal force in the absence of friction. The components of the normal force N in the horizontal and vertical directions must equal the centripetal force and the weight of the car, respectively. In cases in which forces are not parallel, it is most convenient to consider components along perpendicular axes—in this case, the vertical and horizontal directions.
[link] shows a free body diagram for a car on a frictionless banked curve. If the angle is ideal for the speed and radius, then the net external force will equal the necessary centripetal force. The only two external forces acting on the car are its weight and the normal force of the road . (A frictionless surface can only exert a force perpendicular to the surface—that is, a normal force.) These two forces must add to give a net external force that is horizontal toward the center of curvature and has magnitude . Because this is the crucial force and it is horizontal, we use a coordinate system with vertical and horizontal axes. Only the normal force has a horizontal component, and so this must equal the centripetal force—that is,

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?