| << Chapter < Page | Chapter >> Page > |
In this case, there is no initial horizontal separation. Projectiles are thrown from different levels. Both projectiles travel same horizontal distnace for all time. Clearly, relative velocity in horizontal i.e x-direction is zero :
On the other hand, time of collision is obtained by considering relative motion in y-direction :
Problem : A fighter plane is flying horizontally at a speed of 360 km/hr and is exactly above an aircraft gun at a given moment. At that instant, the aircraft gun is fired to hit the plane, which is at a vertical height of 1 km. If the speed of the shell is 720 km/hr, then at what angle should the gun be aimed to hit the plane (Neglect resistance due to air)?
Solution : This is a case of collision between fighter plane and shell fired from the gun. Since plane is overhead, it is required that horizontal component of velocity of the shell be equal to that of the plane as it is flying in horizontal direction. This will ensure that shell will hit the plane whenever it rises to the height of the plane.
Two projectiles
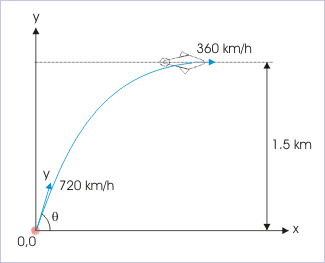
Now the horizontal and vertical components of shell velocity are :
For collision,
However, we need to check that shell is capable to rise to the height of the plane. Here,
The maximum height achieved by the shell is obtained as here :
The shell indeed rises to the height of the plane (1000 m) and hence will hit it.
Problem : Two projectiles are projected simultaneously from a point on the ground “O” and an elevated position “A” respectively as shown in the figure. If collision occurs at the point of return of two projectiles on the horizontal surface, then find the height of “A” above the ground and the angle at which the projectile "O" at the ground should be projected.
Relative motion

Solution : There is no initial separation between two projectiles in x-direction. For collision to occur, the relative motion in x-direction should be zero. In other words, the component velocities in x-direction should be equal so that two projectiles cover equal horizontal distance at any given time. Hence,
Relative motion

We should ensure that collision does occur at the point of return. It means that by the time projectiles travel horizontal distances required, they should also cover vertical distances so that both projectiles are at “C” at the same time. In the nutshell, their times of flight should be equal. For projectile from "O",
For projectile from "A",
For projectile from "A",
Squaring both sides and putting values,
We have deliberately worked out this problem taking advantage of the fact that projectiles are colliding at the end of their flights and hence their times of flight should be equal. We can, however, proceed to analyze in typical manner, using concept of relative velocity. The initial separation between two projectiles in the vertical direction is “H”. This separation is covered with the component of relative velocity in vertical direction.
Now, time of flight of projectile from ground is :
Hence, the vertical displacement of projectile from "A" before collision is :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?