| << Chapter < Page | Chapter >> Page > |
Projectile motion
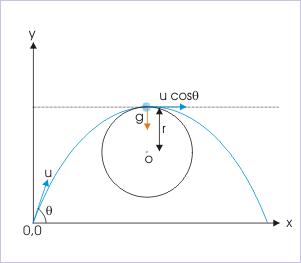
Let radius of curvature of the projectile trajectory at maximum height be “r”, then
A particle moves along a circle of radius “r” meter with a time period of “T”. The acceleration of the particle is :
(a) (b) (c) (c)
In order to determine centripetal acceleration, we need to find the speed of the particle. We can determine the speed of the particle, using expression of time period :
The acceleration of the particle is :
Hence, option (a) is correct.
Which of the following quantities are constant in uniform circular motion :
(a) velocity and acceleration
(b) magnitude of acceleration and radius of the circular path
(c) radius of the circular path and speed
(d) speed and acceleration
Three quantities, namely, radius of the circular path, magnitude of acceleration and speed are constant in uniform circular motion.
Hence, options (b) and (c) are correct.
Which of these is/are correct for a particle in uniform circular motion :
(a) the acceleration of the particle is tangential to the path
(b) the acceleration of the particle in the direction of velocity is zero
(c) the time period of the motion is inversely proportional to the radius
(d) for a given acceleration, velocity of the particle is proportional to the radius of circle
The options (a), (c) and (d) are wrong.
Hence, option (b) is correct.
A particle moves with a speed of 10 m/s along a horizontal circle of radius 10 m in anti-clockwise direction. The x and y coordinates of the particle is 0,r at t = 0. The velocity of the particle (in m/s), when its position makes an angle 135° with x - axis, is :
(a) (b) (c) (d)
The velocity is a vector quantity. We need to know the components of the velocity when particle makes the angle 135° with x - axis.
Uniform circular motion
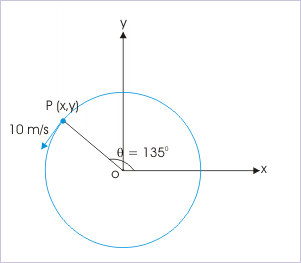
The component is in the reference x - direction, whereas component is in the negative reference y - direction.
Hence, option (a) is correct.
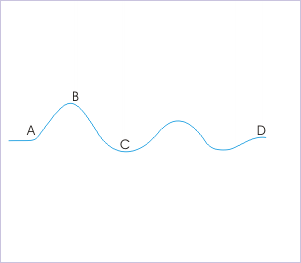
A car moves along a path as shown in the figure at a constant speed. Let , , and be the centripetal accelerations at locations A,B,C and D respectively. Then
Uniform circular motion
(a) (b) (c) (d)
The curvatures of path at four points are indicated with our circles drawn so that they align exactly with the curved path at these points. The radii of these circles at points A and B are smaller than that at points C and D.
Uniform circular motion
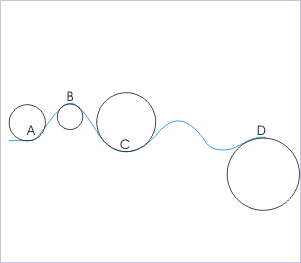
Now, the centripetal acceleration is given by :
The smaller the radius, greater is centripetal acceleration. Thus,
and
Hence, options (b) and (d) are correct.
A particle executes uniform circular motion with a speed “v” in xy plane, starting from position (r,0), where “r” denotes the radius of the circle. Then
(a) the component of velocity along x - axis is constant
(b) the component of acceleration along x - axis is constant
(c) the angle swept by the line joining center and particle in equal time interval is constant
(d) the velocity is parallel to external force on the particle
The component of velocity along x - direction is “-v sinθ” and is not a constant. The component of acceleration along x - direction is “ ” and is not a constant. The external force in uniform circular motion is equal to centripetal force, which is directed towards the center. Thus, the velocity is perpendicular to external force.
On the other hand, the particle covers equal circular arc in equal time interval. Hence, the angle subtended by the arc at the center is also equal in equal time interval.
Hence, option (c) is correct.
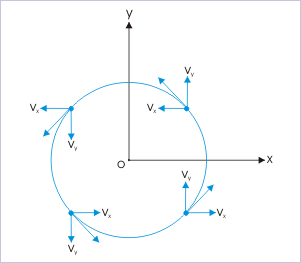
A particle executes uniform circular motion with a speed “v” in anticlockwise direction, starting from position (r,0), where “r” denotes the radius of the circle. Then, both components of the velocities are positive in :
(a) first quadrant of the motion
(b) second quadrant of the motion
(c) third quadrant of the motion
(d) fourth quadrant of the motion
From the figure, it is clear that the components of velocity in the fourth quadrant are both positive.
Uniform circular motion
Hence, option (d) is correct.
A particle executes uniform circular motion with a constant speed of 1 m/s in xy - plane. The particle starts moving with constant speedfrom position (r,0), where "r" denotes the radius of the circle. If center of circle is the origin of the coordinate system, then what is the velocity in"m/s" of the particle at the position specified by the coordinates (3m,-4m) ?
(a) (b) (c) (d)
Here, the inputs are given in terms of coordinates. Thus, we shall use the expression of velocity, which involves coordinates. Velocity of the particle in circular motion is given by :
Uniform circular motion
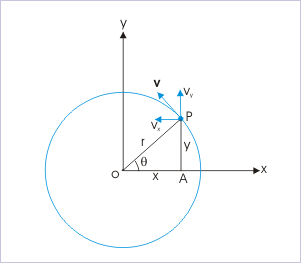
Here, radius of the circle is :
Hence, option (a) is correct.

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?