Center of mass  (Page 5/3)

Our study of motion has been limited up to this point. We referred particle, object and body in one and same way. We considered that actual three dimensional rigid body moved such that all constituent particles had same motion i.e. same trajectory, velocity and acceleration.

An actual body, however, can move differently to this simplified paradigm. Consider a ball rolling down an incline plane or consider a stick thrown in air. Different parts of the body have different motions. While translating in the air, the stick rotates about a moving axis. In the nutshell, this means that these bodies may not behave like a particle as assumed earlier.

Stick thrown in air

Apparently, it would be quite complicated to describe motions of parts or particles, having different motions, in an integrated manner. There is but one surprising simplifying characteristic of these motions. There is a characteristic geometric point of the three dimensional body in motion, which behaves yet as a particle. This point is known as "center of mass" in short "COM". It has following two characterizing aspects :

• COM appears to carry the whole mass of the body.
• All external forces appear to apply at COM.

Rolling ball on an incline and stick thrown in air

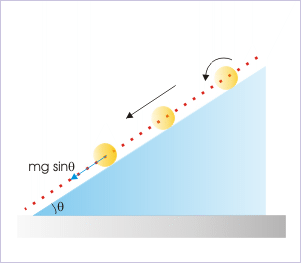
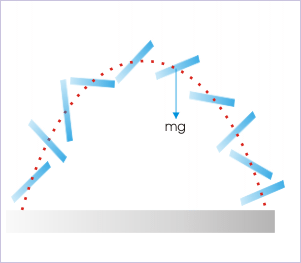
Significantly, the center of ball, which is COM of rolling ball, follows a straight linear path; whereas the COM of the stick follows a parabolic path as shown in the figure. Secondly, the forces appear to operate on the COMs in two cases are “mgsinθ” and “mg” as if they were indeed particle like objects. This concept of COM, therefore, relieves us of the complexities that otherwise we would have faced describing motions of rigid bodies.

We must here note the word "appear" in describing characteristics of COM. In reality, COM is a geometric point. It need not be even the part of the body. Think of a hollow sphere, whose center is its COM. Is there any material there? Also, consider the motion of the stick again. Each particle constituting the stick is pulled by gravitational force. What it means that external forces, in actuality, may not act on COM alone as they appear in equivalent term.

Further the concept of COM is equally valid to a system of particles, which may not be in contact. This follows from the fact that a rigid body, after all, is an arrangement of particles, where inter-particle distances are extremely small.

In words, we can, therefore, define COM as :

Center of mass (COM)

COM of a system of particles is a geometric point, which assumes all the mass and external force(s) during motion.

Mathematical expression of com for a system of particles

Let us now look at a baseball bat closely. It has a peculiar shape. Where should the COM lie? By experience, we can say that it should lie on the heavier side. This perception comes from the realization that heavier part has most of the mass. It gives us the clue about COM that it lies on the heavier side of an irregularly shaped body. Now, let us consider the motion of spherical sphere of uniform density. Here, mass is evenly distributed. Where should the COM lie? Obviously, COM coincides with the center of spherical ball.